This is a set of Masyus, a classic logic puzzle. So, we need to use logical
reasoning to deduce what the path of each loop looks like. Below is an
in-depth logical solution for each puzzle; in practice, you typically don't have
to think through the solution this much, and relying on intuition is also a
powerful strategy.
Throughout this solution, we refer to cells by RxCy (row x column y), where
R1C1 is the top left cell and R1C7 is the top right cell.
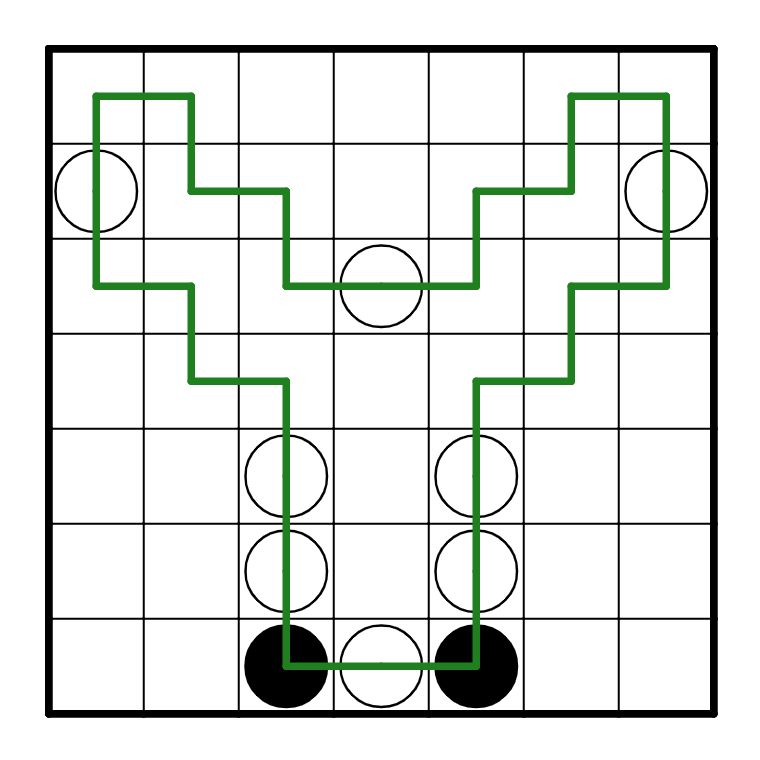
Puzzle 1
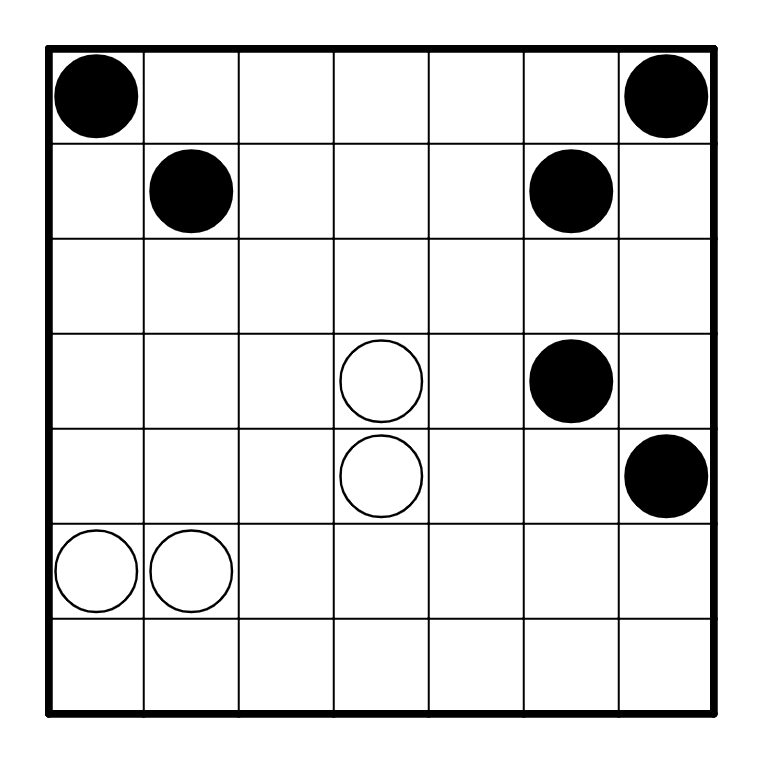
There are several places where you can start this puzzle. In particular, the black
pearls in the corners are useful.
The path must turn on a black pearl. In addition, it must go straight on the next edge.
This means that the path forms an "L" shape of sorts around the black pearls. So, we
can consider what happens to the path when it crosses through R2C2. The path cannot go
up, because if it went up, it would have to go up again and that would hit the edge. A similar
argument can be made for the left side as well. So we know R2C2 has to go right and down. We
can make a symmetric argument for R2C6.
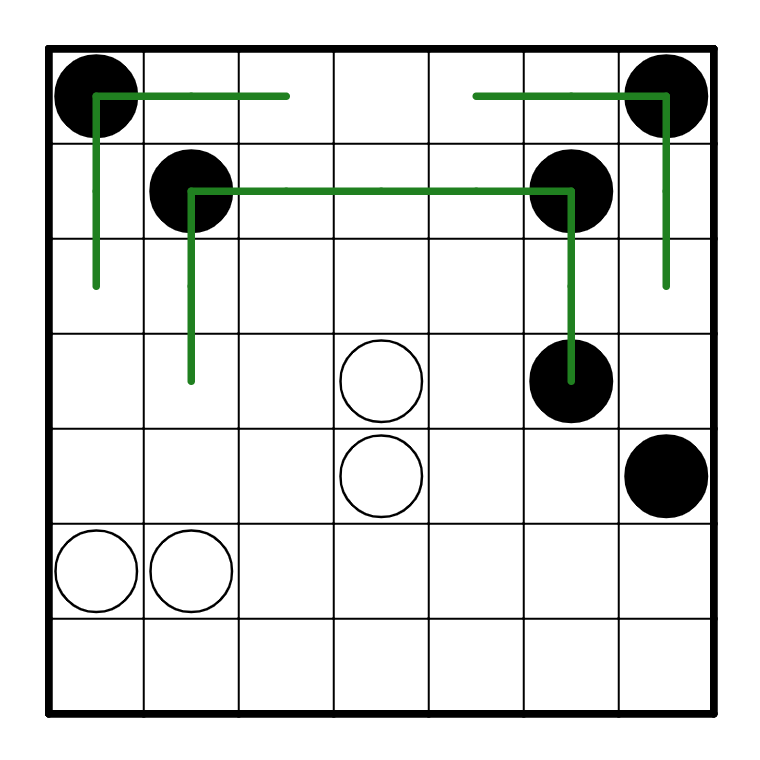
There are still a few more steps we can make with the given pearls. We know the black pearl in
R4C6 needs to turn, but it can't go right for a similar reason to earlier. As such, it needs to
go left. Also, we can consider the black pearl on R5C7. Because the path needs to turn,
it will either go up + left or down + left on that cell, because it can't go right.
Either way, the path is going left.
We can also consider the white cells in the bottom left corner. The path must go straight on a
white pearl, so it either goes straight horizontally or vertically. However, the path cannot
go straight vertically through R6C1 and R6C2, because if it did it would run into the left wall.
So, we know that the path must go horizontally on both of them.
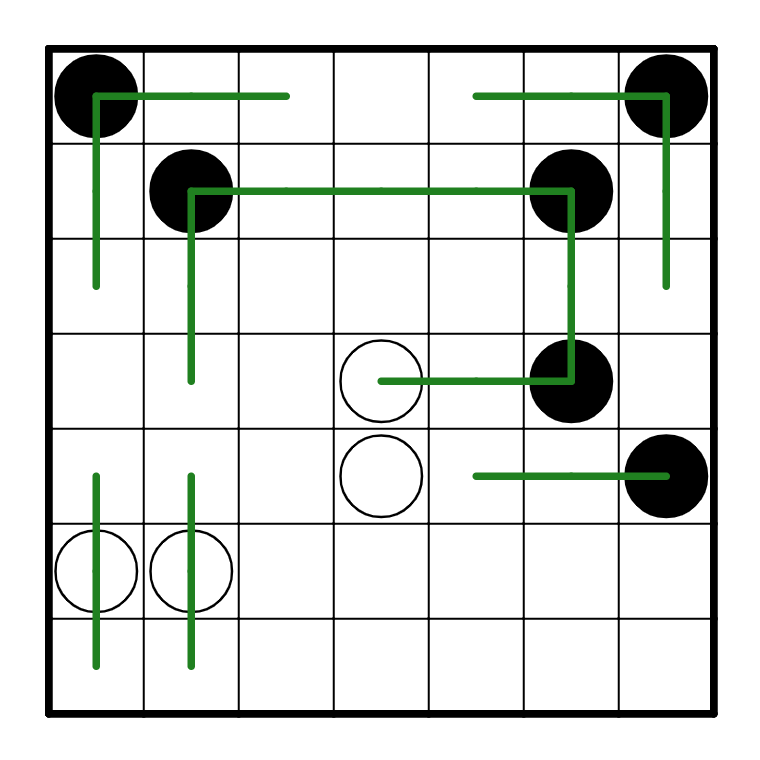
We can also use the knowledge that the path has to connect to itself, without crossing. The
two edges at the top that end at R1C3 and R1C5 have to connect to each other (it's the only way
you could possibly form a loop in the end). We can make a few more deductions like this. Another
deduction that is visible right now is the fact that on R4C4, there is a white pearl, so the path
must go straight through it.
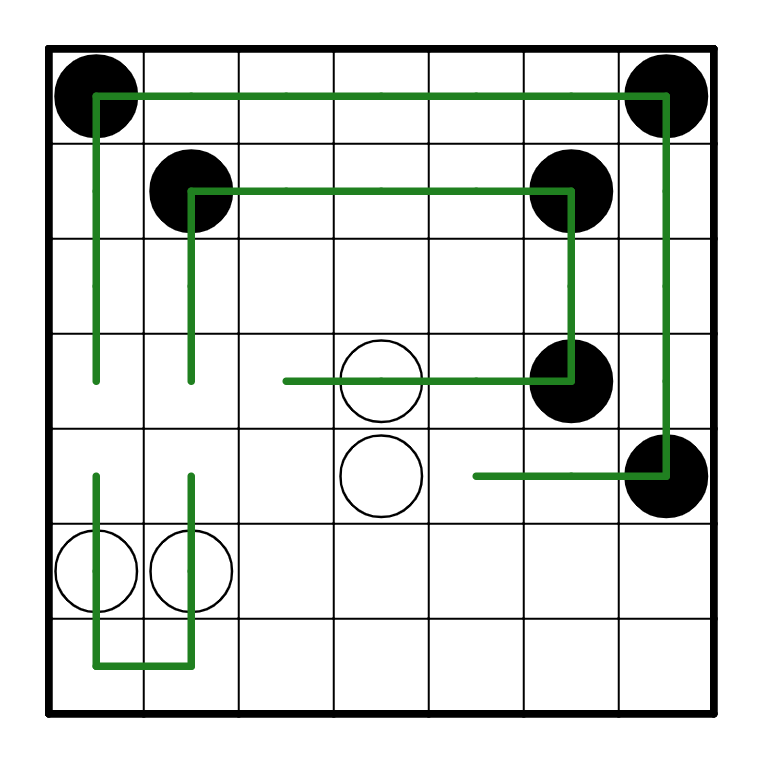
Now, let's look at R4C4 some more. It's a white pearl, which means that the path must turn on
one of the two cells on either side of the path from it. But the path didn't turn on R4C5, so it
has to turn on R4C3! So it either goes up or down. However, we can see that the path can't actually
go up because if it did, it would be trapped with no way to escape. As such, the path goes down.
In addition, there are two other deductions we can make right now. R5C4 is a white pearl, so the path
goes straight through it. But it can't go straight vertically because that would cause the path to
cross itself on R4C4, so it has to be horizontal. Another deduction is what happens to R5C1.
If R5C1 were to turn right, then it would form a small loop in the bottom left. But there has to only
be a single loop throughout the entire puzzle, so this is illegal, and R5C1 has to go up.
From here, the rest of the path is trivial, and the solution is as follows:
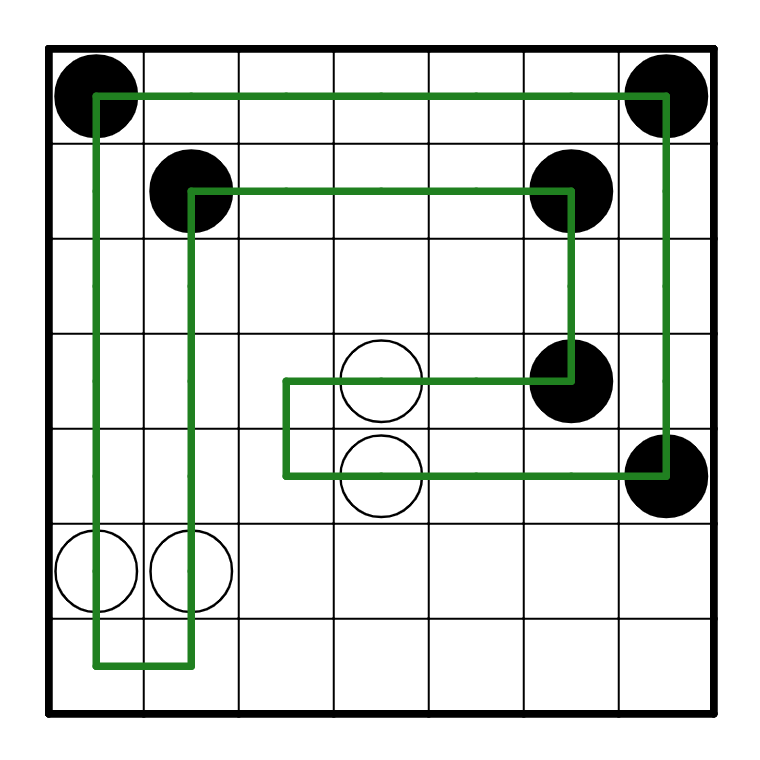
Puzzle 2
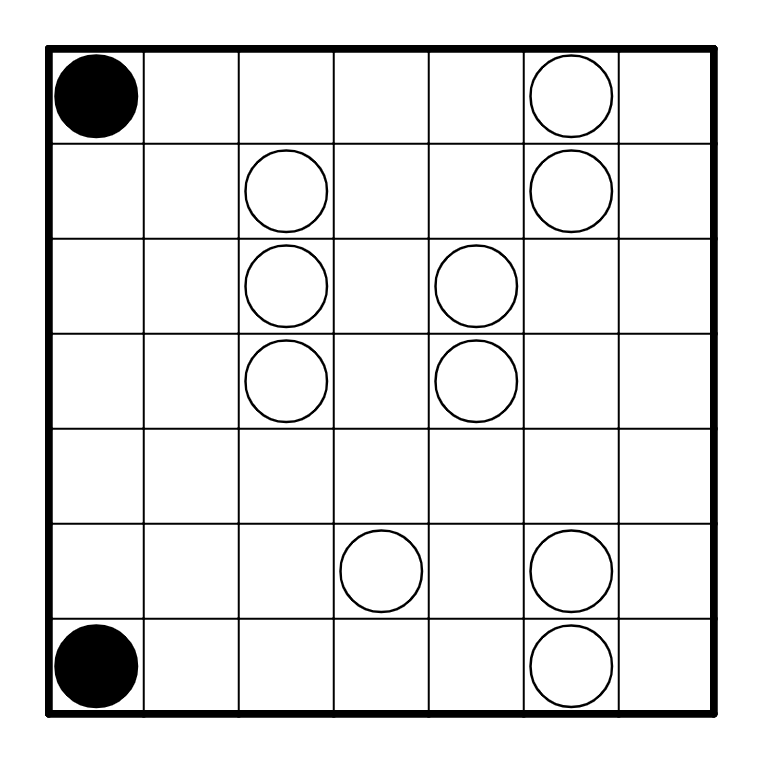
We start out by making some of the deductions we know from the previous puzzle, resolving the
black pearls at R1C1 and R7C1, and resolving some white pearls in R1C6, R2C6, R6C6, and R7C6:
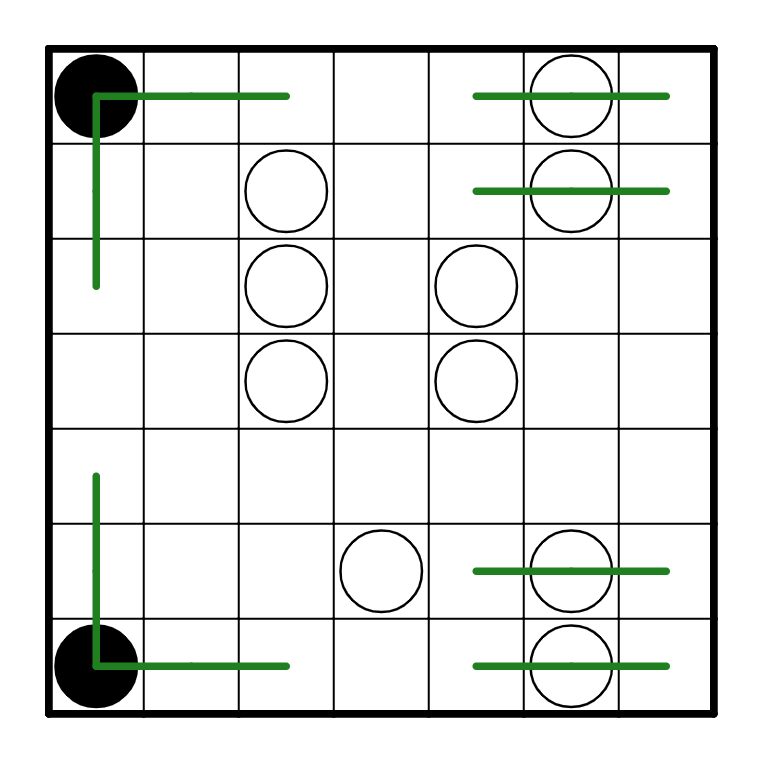
Now, one interesting deduction we can make is at the white pearls in R2C3, R3C3, and R4C3.
In particular, let's look at R3C3, which is a straight line, either horizontal or vertical.
If R3C3 were to be a straight vertical line, then the path would cross through R2C3 and R4C3
next to it. However, the path would have to go straight on both of these, and R3C3 being a
white pearl means that there needs to be a turn next to it. Thus, R3C3 has to be horizontal.
In fact, R2C3 and R4C3 have to be horizontal too (if they were vertical, they'd cross R3C3).
So now we have:
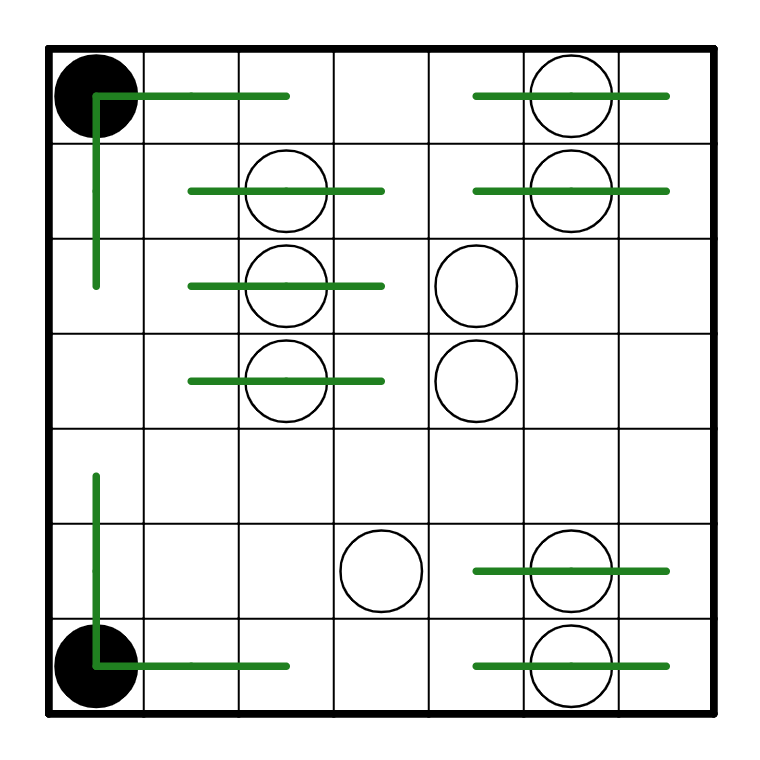
We can also make some deductions based on path connectivity. For instance, R7C7 has to go up.
However, R7C5 can't also go up because that would cause a small loop in the bottom right, so
R7C5 goes left. In fact, we can repeat this deduction on the top right, connecting R1C5 with
R1C3 (which can only go right currently), and then an identical argument can be made on
R2C2 and R2C4. In the end, we're left with this:
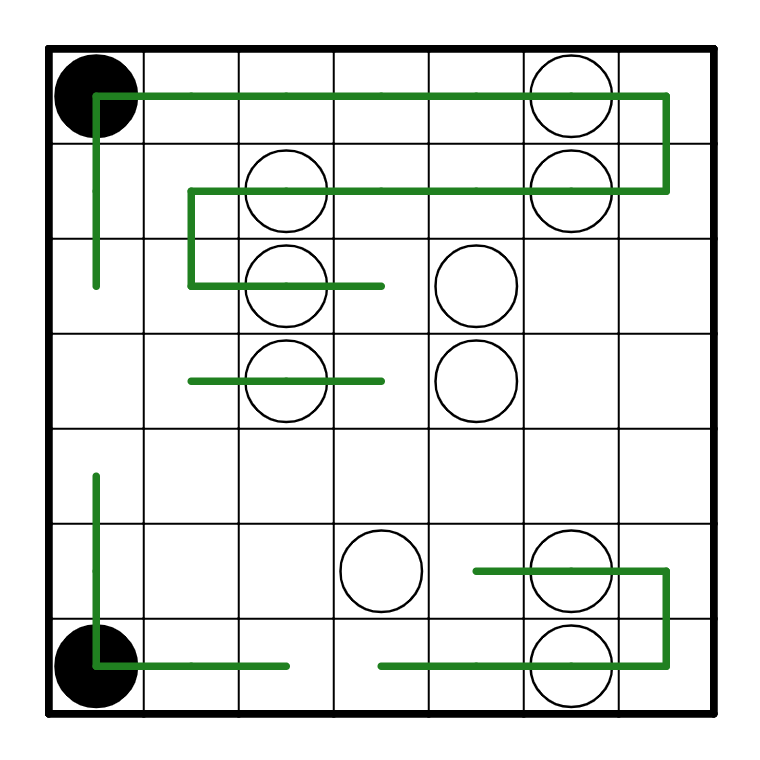
Because R3C5 is a white pearl, it has to go straight; it can't go straight vertically, so
it must be horizontal. In addition, because the loop doesn't turn on the previous cell (R3C4),
it must turn on the next on (R3C6) and go down. The white pearl on R4C5 similarly needs to be
horizontal, and it connects to the path above it.
From here, we can observe that R4C2 needs to turn because of the white pearl on R4C3. Then, we
can connect the loop between cells R3C1 and R5C1 because that's the only way that R3C1 can
connect with the rest of it to yield:
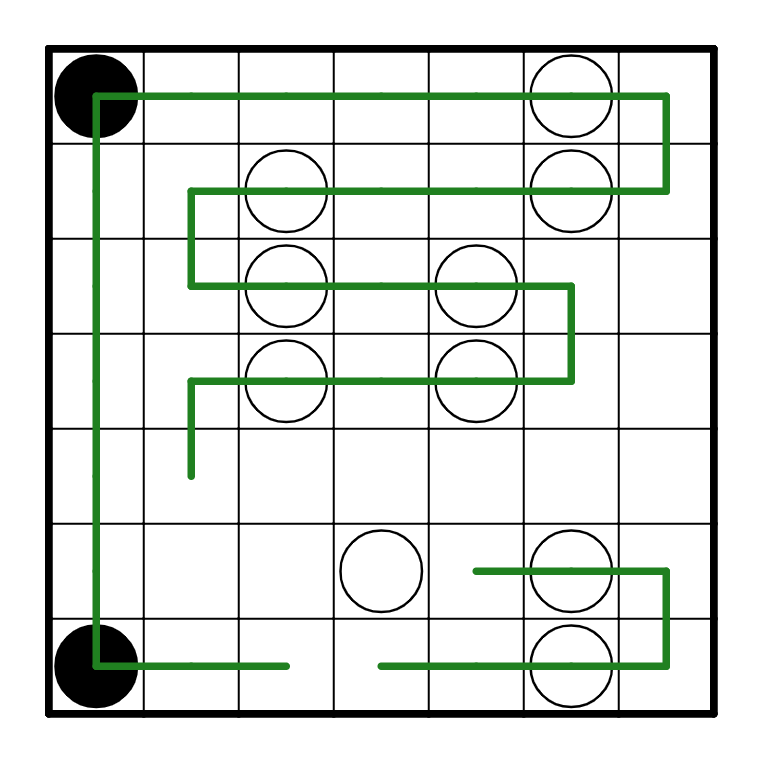
The solution is pretty guessable from here, but the final logical step is to observe what happens
if R6C4 is a vertical straight line. If that happens, then how will R6C5 connect with the rest of
the loop? Well, it would have to run into R5C4, which would form a smaller loop. As such, it
needs to go straight. Simple Masyu rules take care of the rest, and we've arrived at the solution:
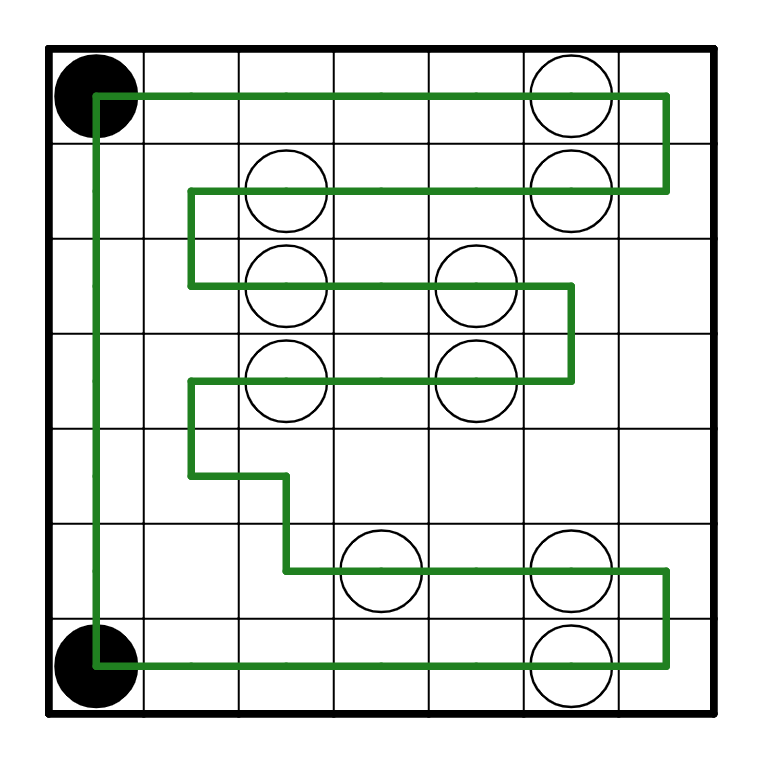
Puzzle 3
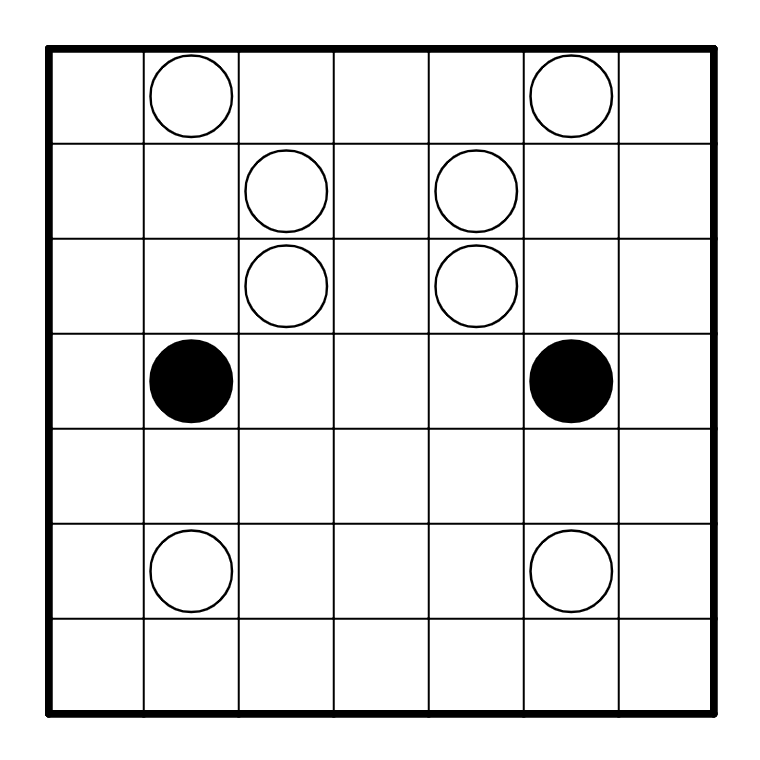
Well, now the puzzle is slightly tricker, because there are two loops. This makes it harder to
use connectivity deductions as we did before. However, we can still start the puzzle off
by resolving the white pearls in R1C2 and R1C6. Also, the black pearls have to go towards
the center of the grid (right and left respectively), since if they didn't, they'd have to go
straight running into the wall.
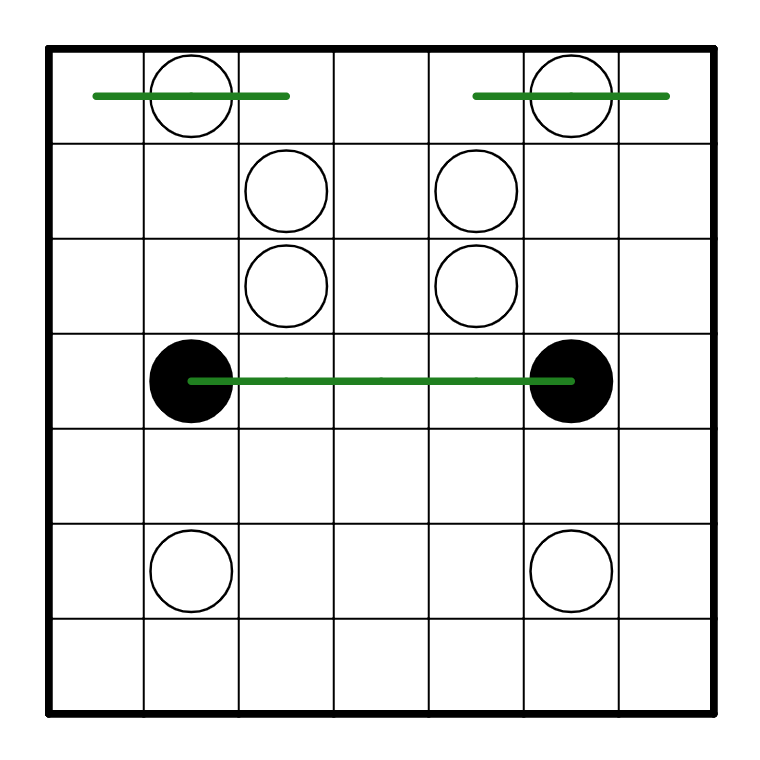
From here, we can resolve the white pearls in R2C3, R2C5, R3C3, R3C5. All of them have to go
horizontally, or else they'd cause the loop to cross at R4C3 or R4C5. In addition, it turns out
they have to connect to each other, because the path needs to turn on R2C2 and R2C6.
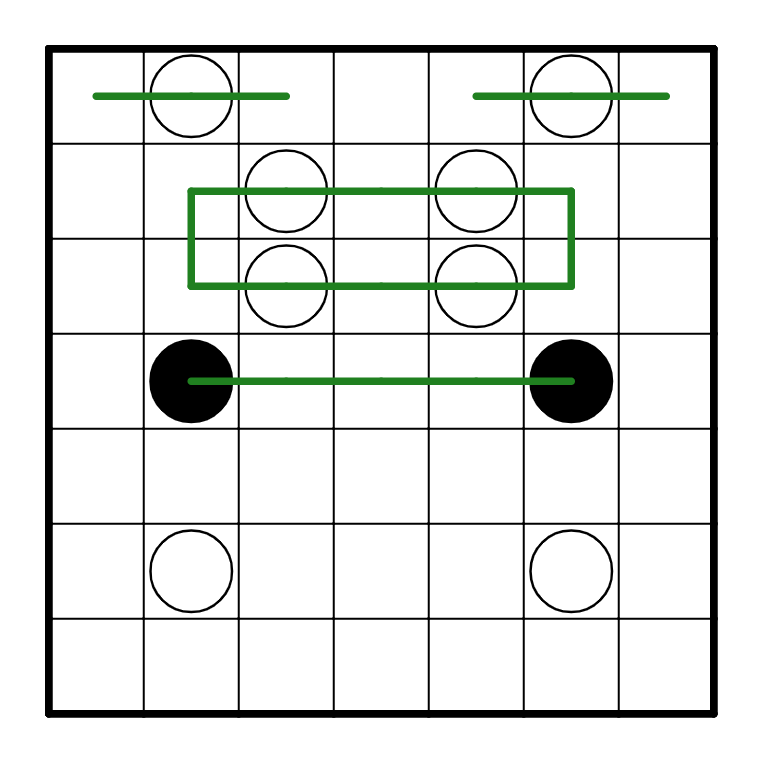
Now the rest of the puzzle resolves quite simply. The black pearls have to go down, and everything
connects neatly around the top.
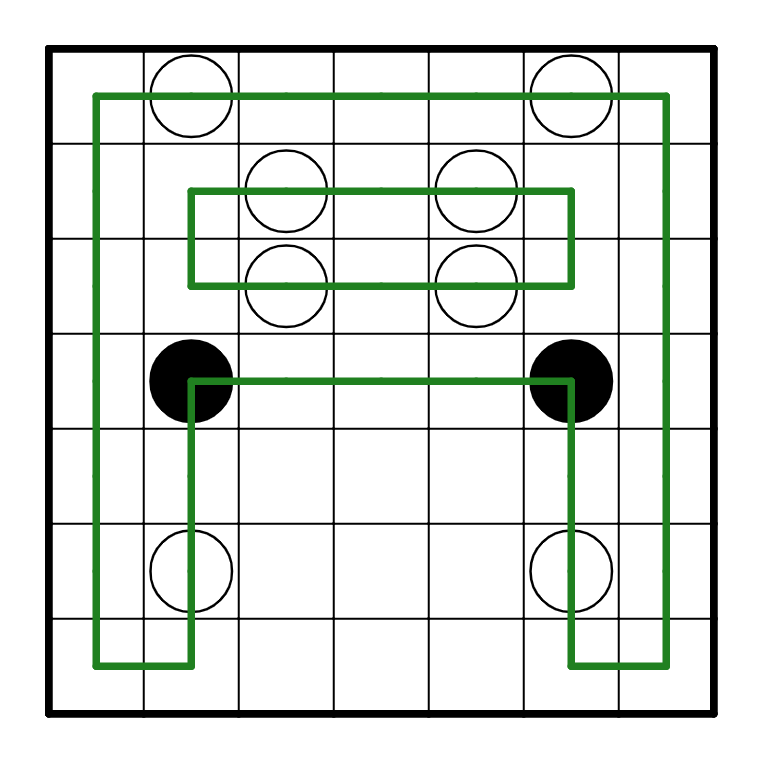
Puzzle 4
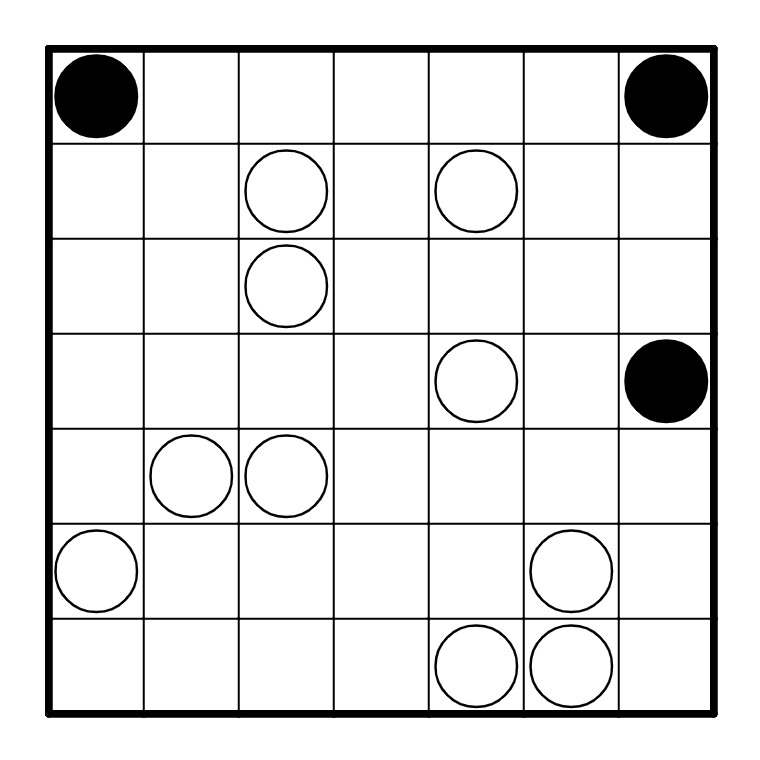
In my opinion, this is the hardest puzzle in this set. We can still start off with a couple of
basic deductions, though, utilizing black and white pearl logic, as well as the fact that
a path that runs into the corner only has one way to escape:
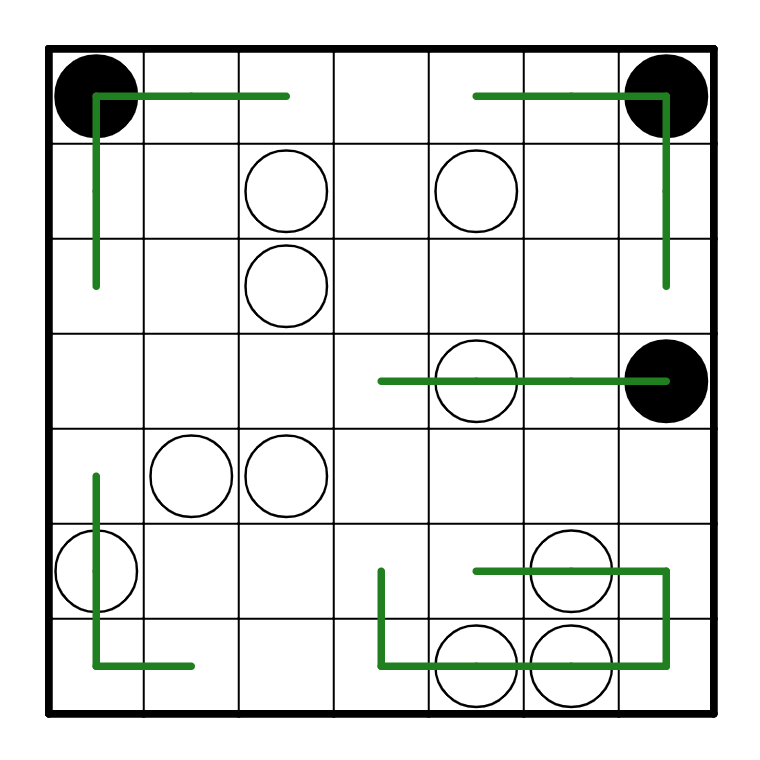
This next step is quite tricky. The easiest way to see what happens is to draw out the path if
the two white pearls in R5C2 and R5C3 both were horizontal. Then, the path at R7C2 is almost
trapped: It can only connect to R6C4. This means that R6C4 needs to go left to meet up with
R7C2.
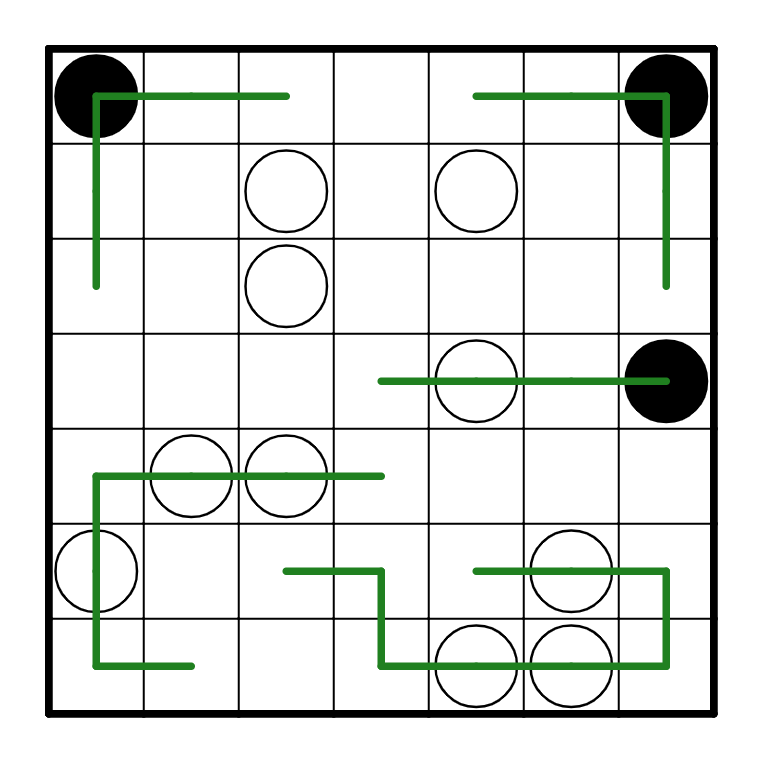
However, this is now a problem: The only way for R6C5 to escape is to go up and then left,
meeting up with R5C4. But this will cause a contradiction in the white cell at R5C3. Therefore,
the assumption that R5C2 and R5C3 were horizontal was wrong, and both of them are vertical.
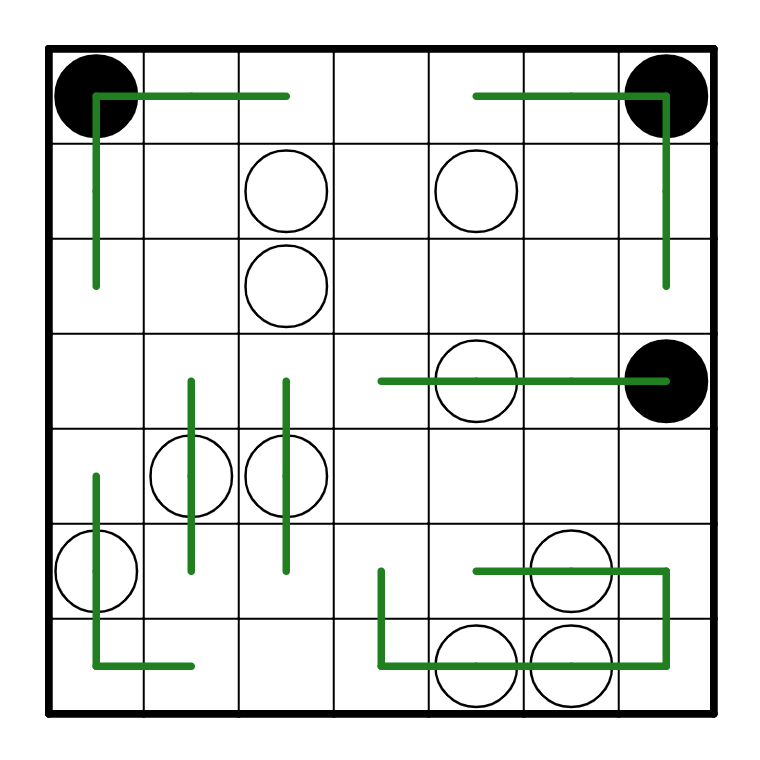
The next step is also a little tricky to see. It concerns R6C4. If R6C4 were to go either up or
right, then the bottom left corner will be a problem: There are three paths in there that
need to connect up, but 3 is an odd number, so there will ultimately be one path that
doesn't connect up to anything. As such, R6C4 needs to go left in order to avoid this
issue in the bottom left. From here, we can make a few more basic path deductions.
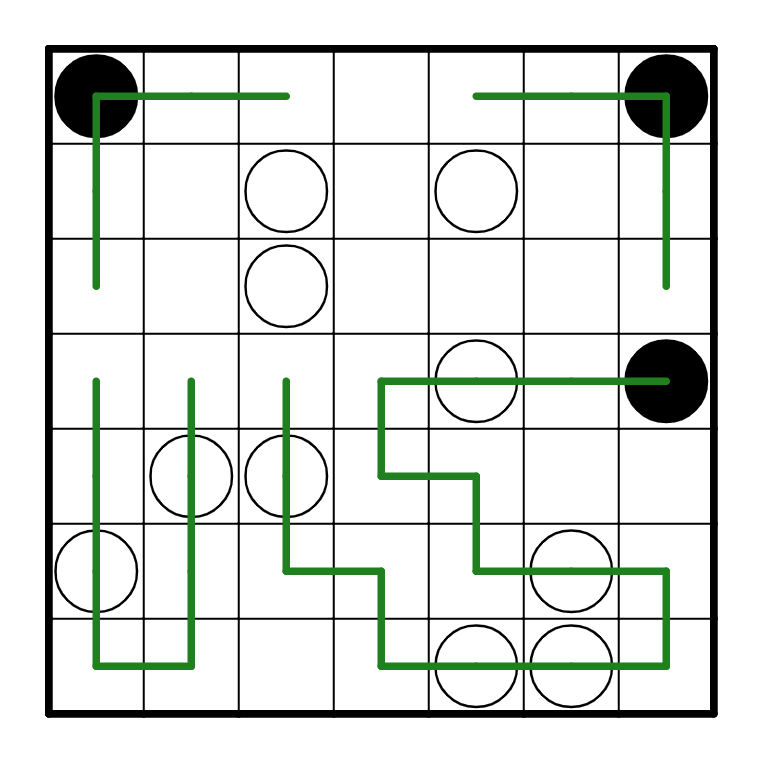
Now, the white pearl at R3C3 can't be horizontal, because if it did, it would connect all the way
up to R3C1, and R3C3 won't satisfy the second part of the white pearl rule. So both R3C3 and R2C3
need to be horizontal. This lets us almost resolve the whole puzzle:
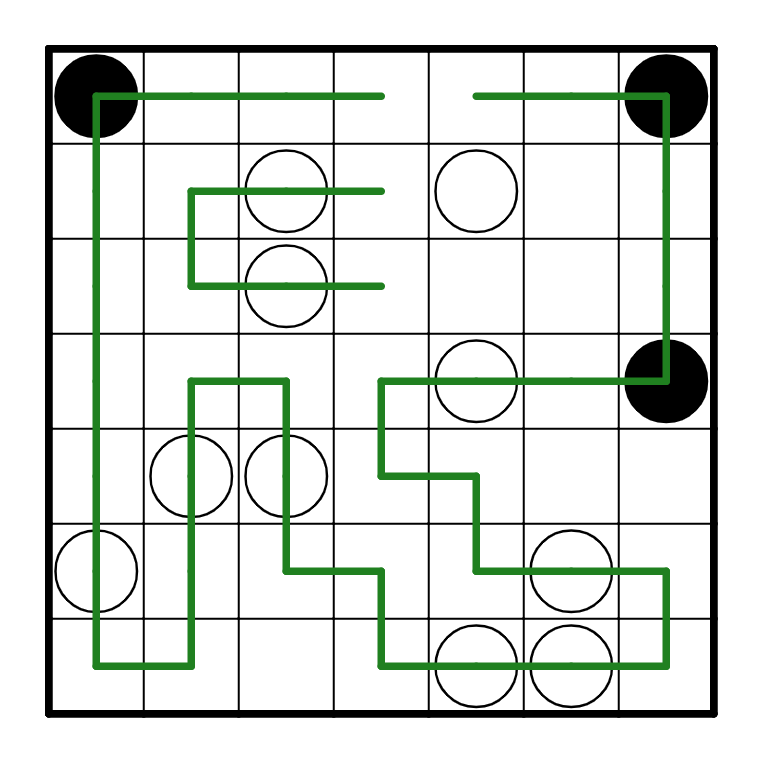
Finally, if R2C5 were to be vertical, then the loop does fully resolve, but it forms only one loop--
recall we need two loops at the end of the puzzle. So the rest of the puzzle does resolve cleanly.
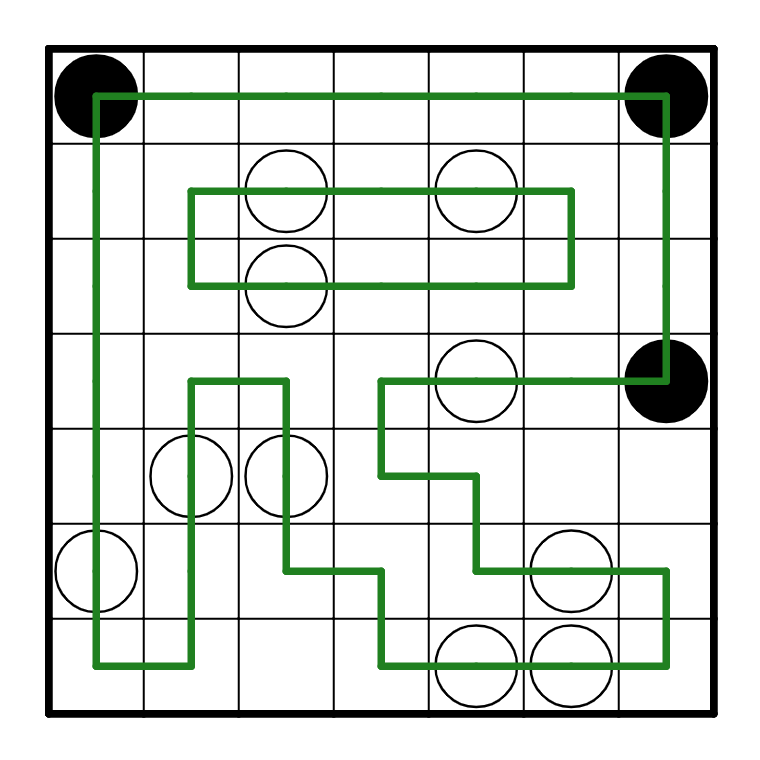
Puzzle 5
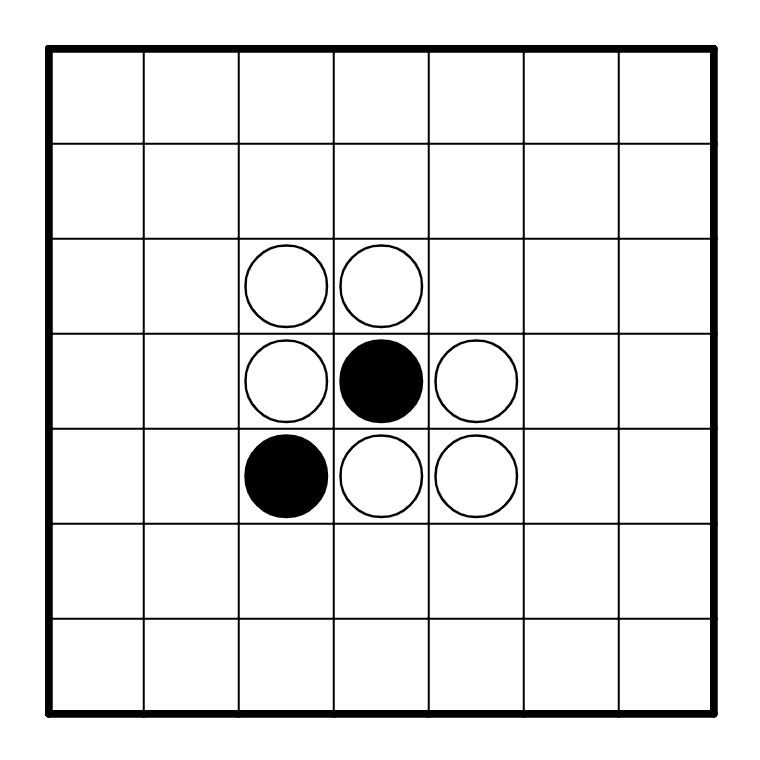
This puzzle is very minimalistic, but the solution is a little more intricate. Total Masyu
is a very powerful constraint, because in many possible loops, there can be white pearls
in multiple different places.
For instance, the black pearl at R5C3 either goes left or right. If it goes left, then
we claim that there should be a white pearl at R5C2. This is because the loop would need to
turn on R5C3, and since it goes straight through R5C2, that cell would satisfy both rules
for a white pearl. As such, R3C3 goes right instead of left, and symmetrically it goes up
instead of down. This also allows us to resolve R4C4 to avoid crossing the loop.
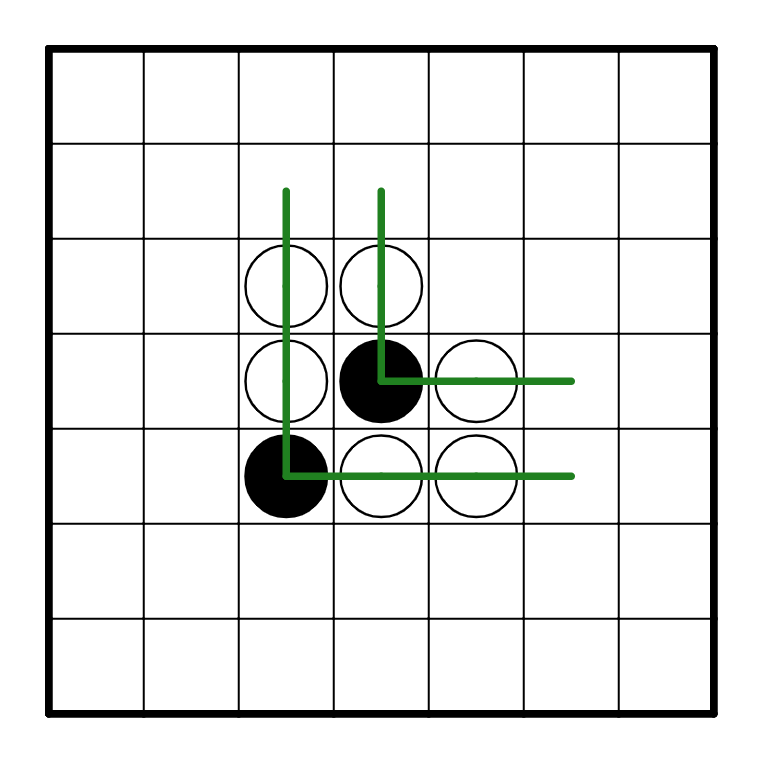
From here it's pretty easy to guess that R3C2 goes right and R5C6 goes up, causing a very small
loop to be formed. The rigorous argument for why this is true is as follows: if R3C2 were to go
left, then the only ways for it to connect back to the other part of the loop is to either go
straight L-R through R1C3 or go straight U-D through R5C7. However, both of these scenarios
would force there to be a white pearl, somewhere in the top row or the right column respectively.
(Try it and see!) So the whole puzzle is resolved.
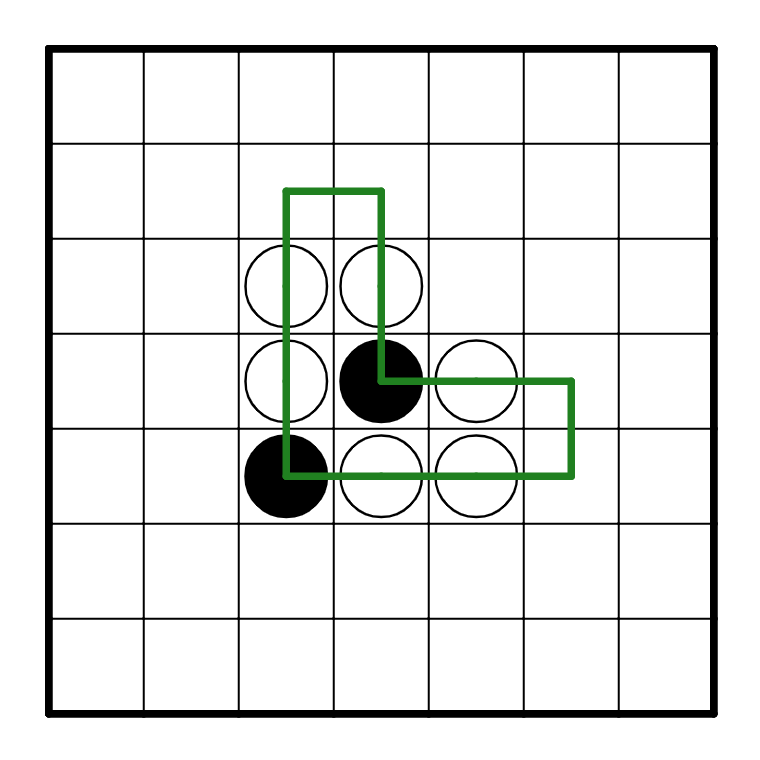
Puzzle 6
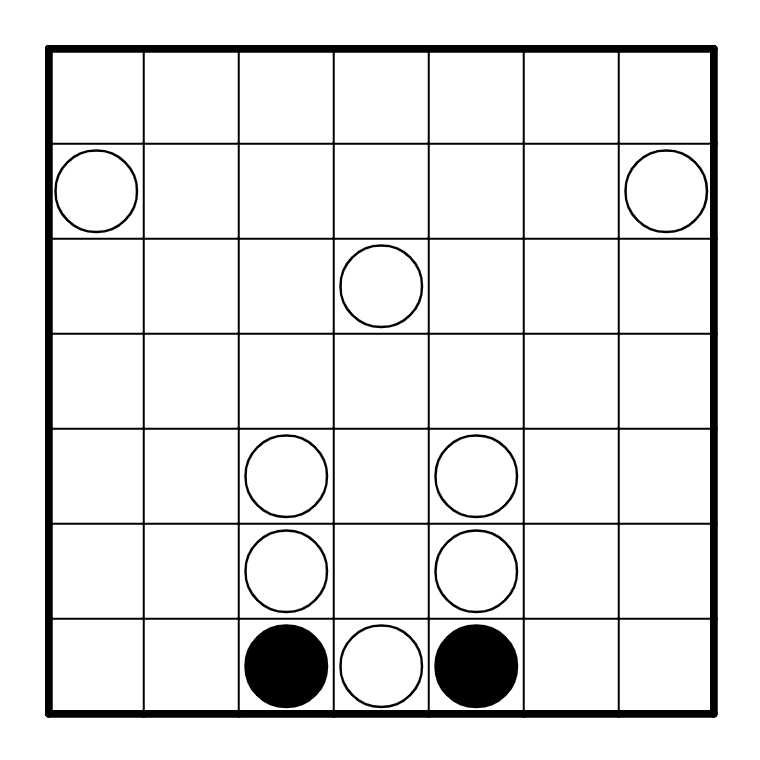
As always, we can start by making some trivial deductions.
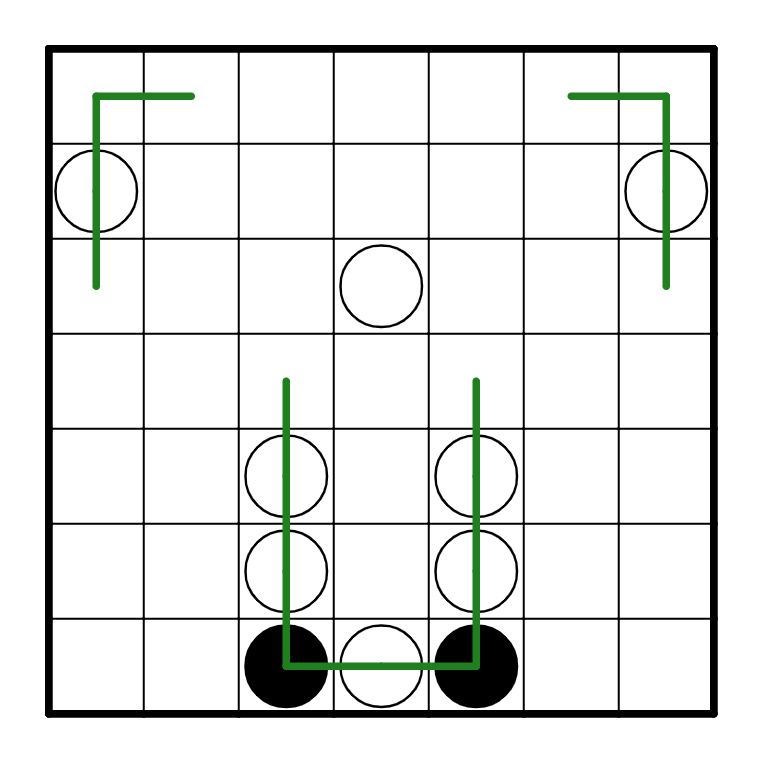
Now, consider R1C2. The cell next to it (R1C1) turns, so if it were to go straight, then
there would be a white pearl at R1C2, which doesn't exist. So R1C2 has to turn, and similarly
R1C6 has to as well. As a trickier step to see, R3C1 has to turn as well. If R3C1 went straight,
then it would have to turn away from Column 1 eventually, and when it does, there would be
a white pearl placeable there. Avoiding small loops gets us to this:
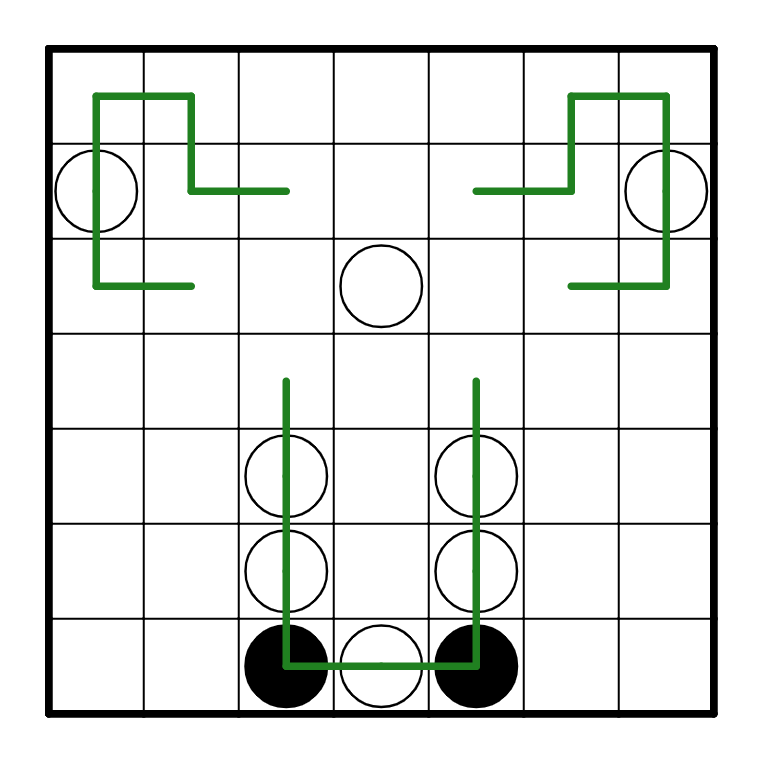
A similar deduction to R1C2 can be made on R3C2. It has to turn in order for there not to be
a white pearl placed on R3C2 in the final solution, because R3C1 turns. This gives us the
connection between R3C2 and R4C3, and similarly the connection between R3C6 and R4C5. From
here, the rest of the solution resolves because R3C5 has to go L-R to avoid getting itself
trapped in the bottom.
Now that we have solved all six of the puzzles, we can extract a final answer. Each puzzle's solution clearly spells out a single letter. In order, they form the word PEARLY, the answer to this puzzle.