Answers for this puzzle:
- ADELSKALENDER
- DIALOGUES
- LONESOME
- MARCHED
- MARGARET BUSBY
- MARIELLA
- NATIONAL ANTHEM
- PANCHEN
- TITANATE
- WHAT I DO THE BEST
We are presented with a Moon or Sun logic puzzle.
The full logical solution is in the appendix, but the solution is here:
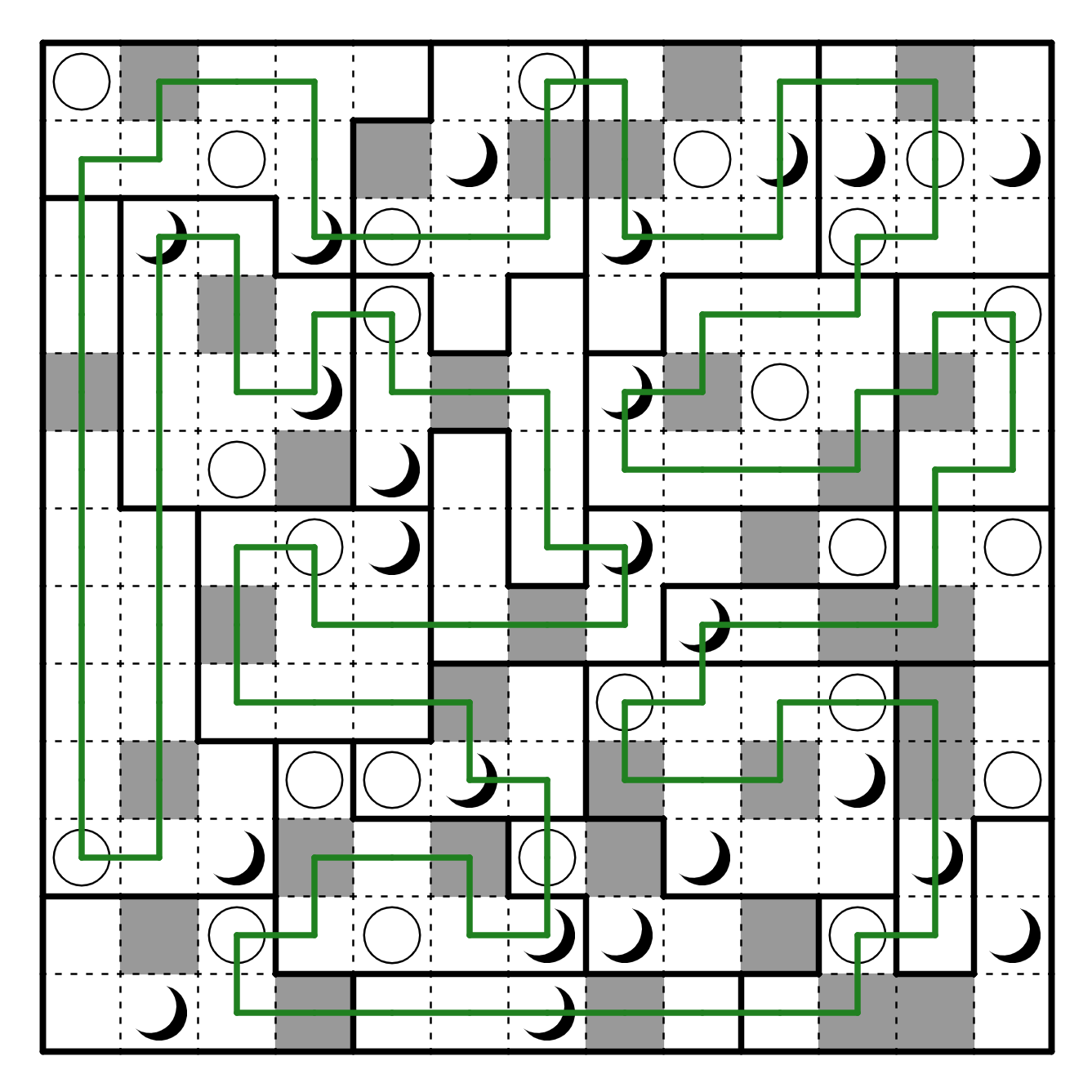
Clued by "names" in the flavortext and "luna"-cy, this is a puzzle about
the names of moons in the Solar System. Each answer used in this puzzle
contains the name of one or two moons in it (e.g. TITANate).
The 10 answers can be placed along the loop, in a counterclockwise direction,
in the moon regions, so that the moon names coincide with the locations of
moons in the grid (and are just treated as a single character):
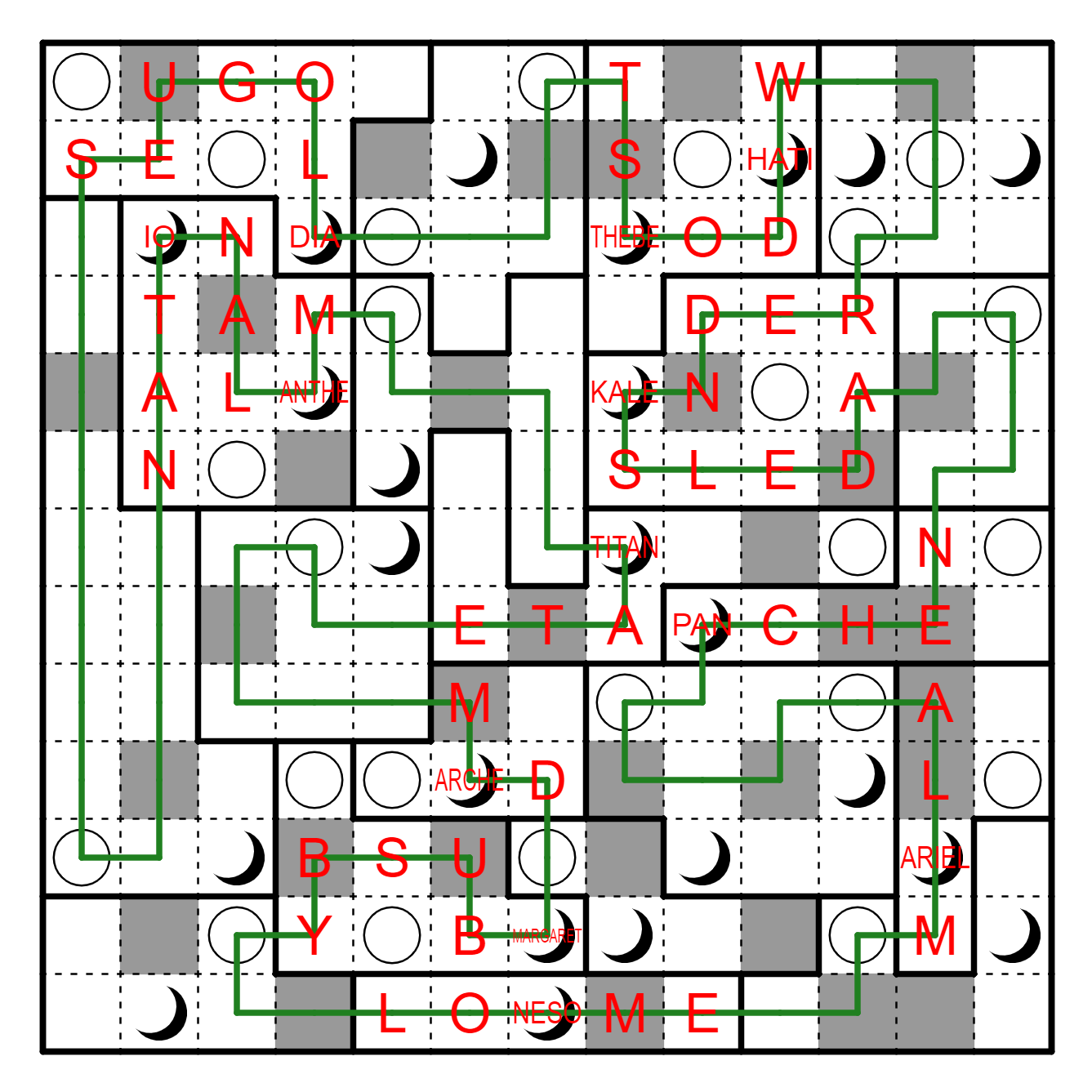
Reading the crossed-over shaded letters in order yields US AND THEM ALBUM,
which clues the answer, the Pink Floyd album
THE DARK SIDE OF THE MOON.
Author's Notes
The dataset of moon names is my favorite source for character names, so when I saw that this was a possible answer for Solidarity, and I could do a puzzle using it to make the answer thematic, I really wanted to make that construction work. It took me a while to come up with an idea for the actual puzzle, though--the first iteration of this was a pretty boring indexing puzzle and only used Jovian moons. I'm happy with the final tie-in to Moon or Sun.
Appendix: Logical solve path
Throughout this solution, we use RxCy to refer to a cell; R1C13 is the
top right cell.

In a Moon or Sun logic puzzle, we can only go through either moons
or suns in each region. Furthermore, we need to alternate. Thus, if
we use moons in the top right region, it will be a problem because
the moon in R2C11 has no way to escape. Thus, that region must use suns.
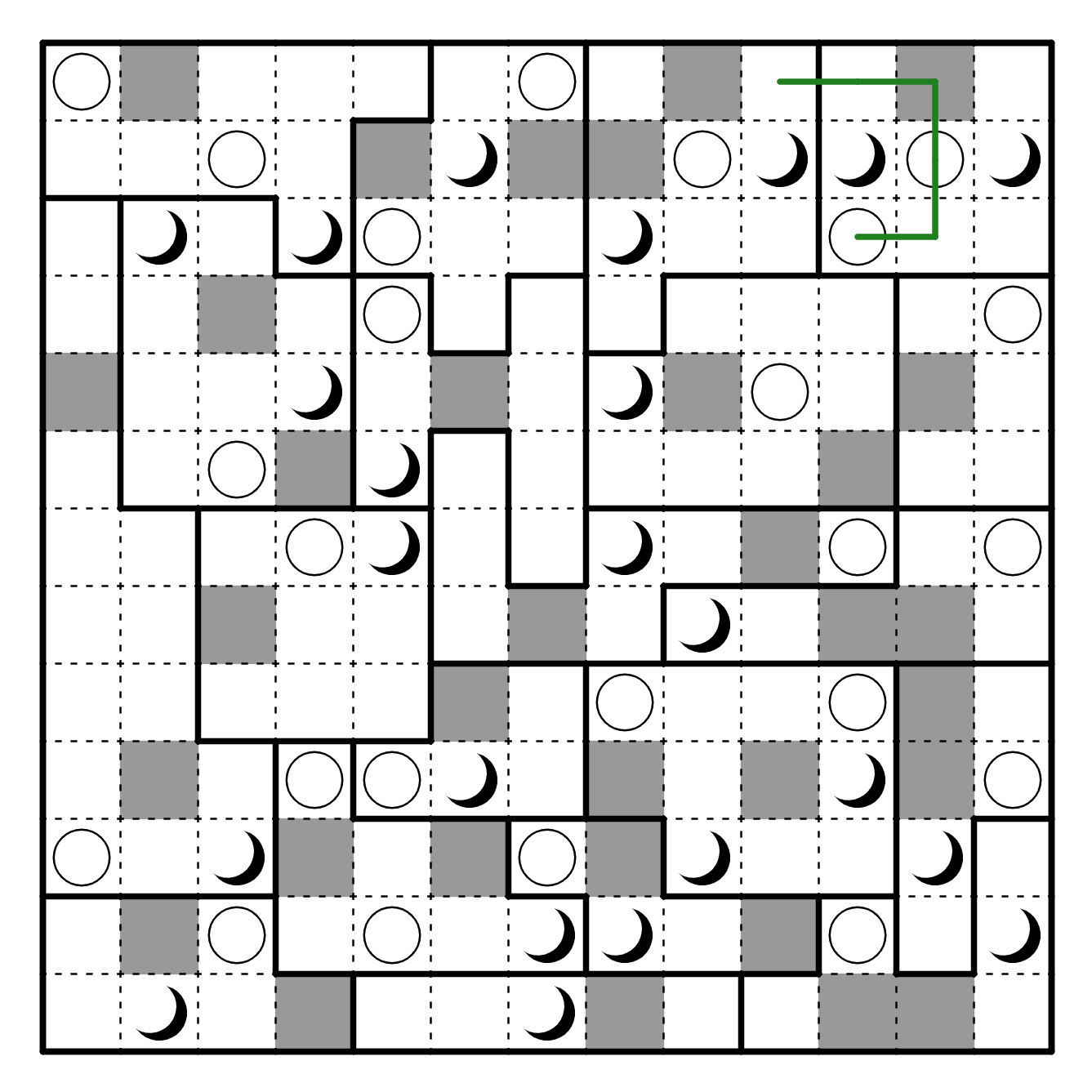
We can now resolve the upper region that is connected to the top right one somewhat;
it needs to visit the two moons in a certain order, otherwise there's no way to
escape the region. The other exit of the top right region must go directly down.
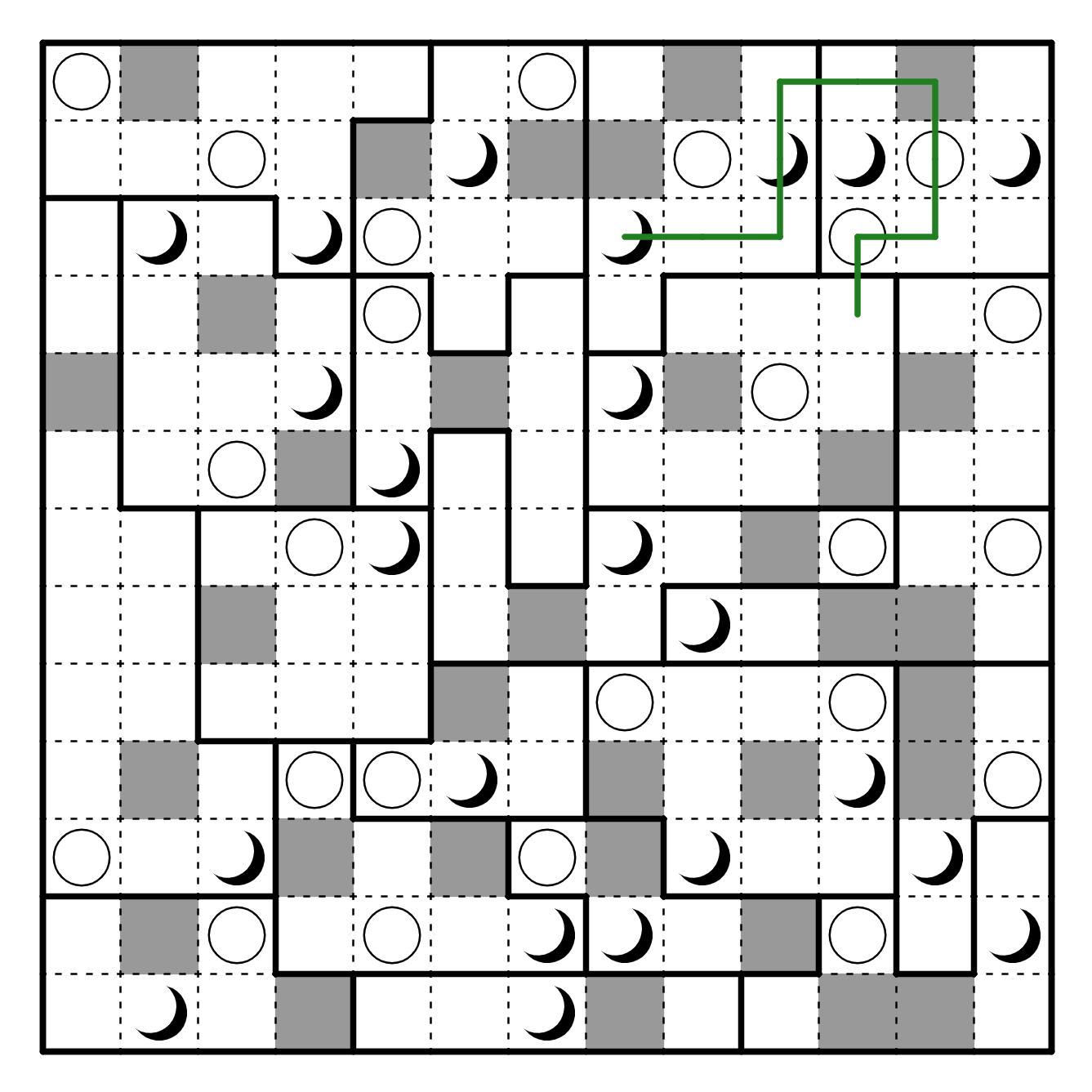
Consider the region including the sun in R4C13. It only is connected to three regions,
and one of those regions we know can't connect to it. Because each region must be
entered and exited, we know when the two entrances to that region is. This lets us resolve
the entire region containing the moon in R5C8. Furthermore, we can resolve the region with the
sun in R4C13 because it has to escape downwards and not through R7C13 since that would
cross both suns. We can also resolve the region that's just entered, since it needs to
go through the moon in there.
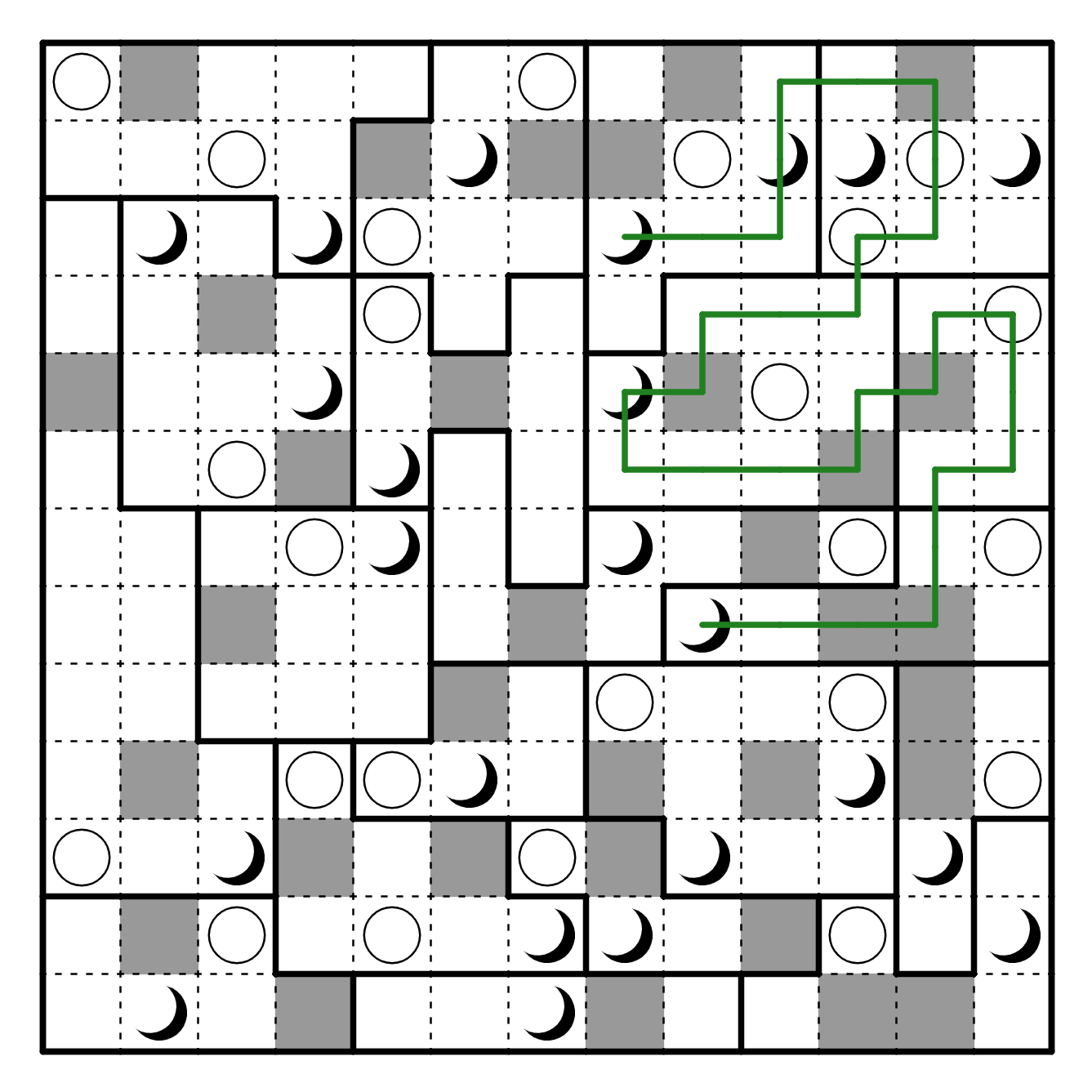
Consider the sun in R7C11. There is no way to visit it, so that region must be a moon region.
Thus the connection R7C7-8 must be used. Also, R8C9 must go down to not
enter the region on a sun visit, and the region it enters from there can be resolved since
there's only one way to visit both suns.
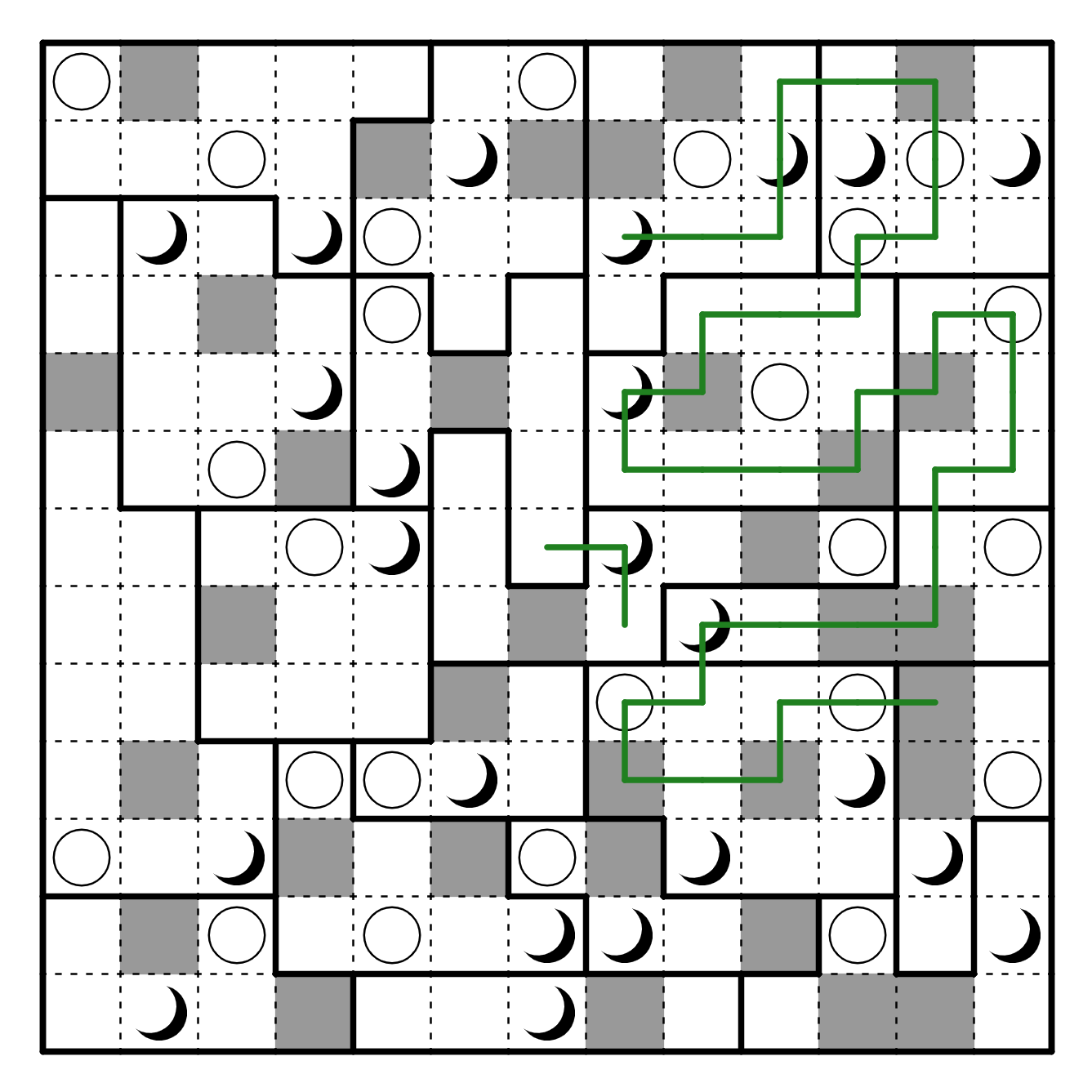
The region containing R7C7 is also resolvable, since it's a sun region. Notably,
this also resolves how the path escapes from R3C8--it must go into the region to the left of that,
and visit both suns. The only way to do this is to escape via the R1C7-8 path.
Since those two regions cannot be directly connected as they're both sun regions,
we need to go left from R4C5, and R3C5 needs to go left as well. Furthermore,
when R3C5 goes left, it cannot exit that region from the region containing R3C2 because
that would once again have two consecutive moon regions. So it needs to exit via R2-3C1.
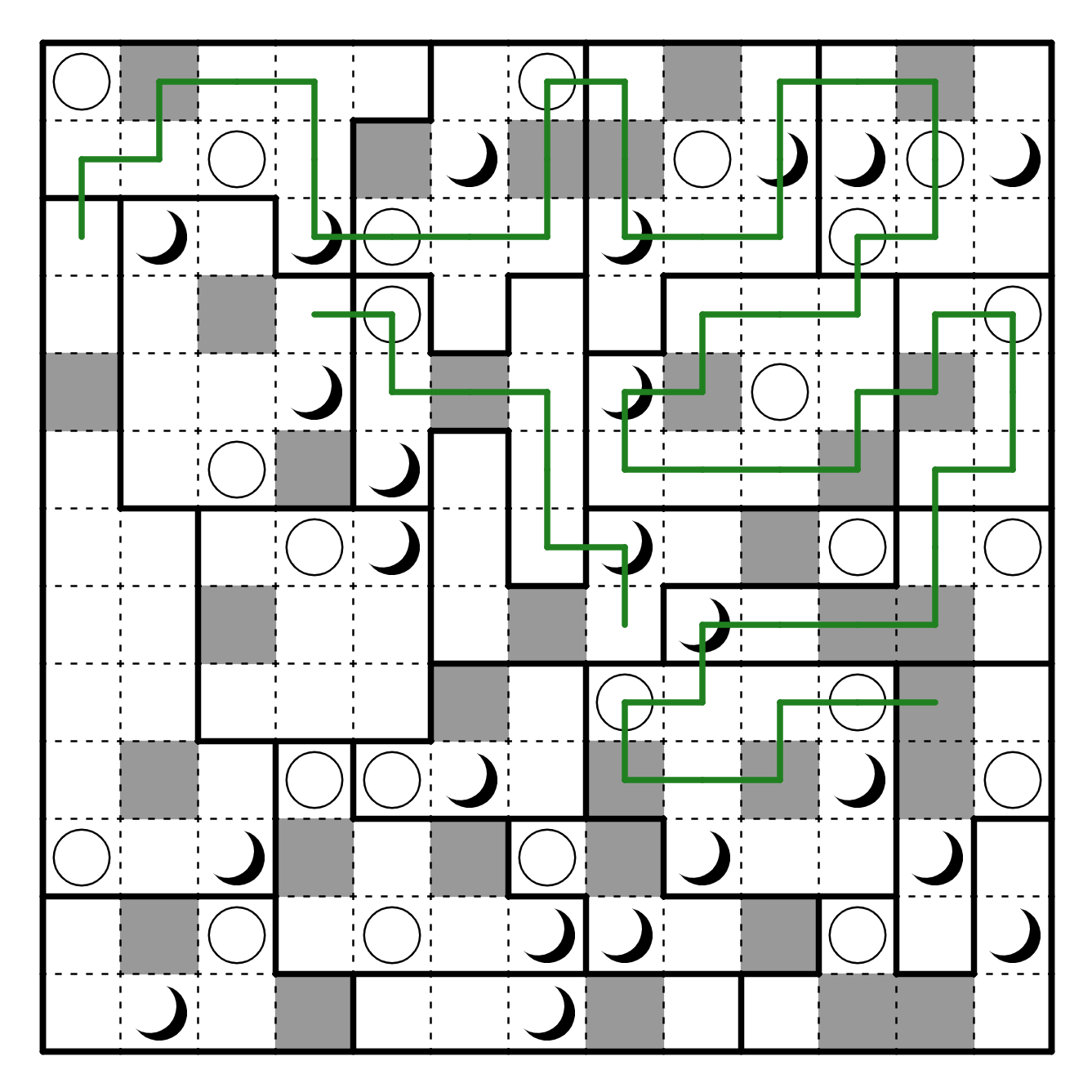
Now, consider R8C8. It cannot exit that region downwards, because there's
no way to visit the sun in the below region without touching the moon. So
it needs to go left. This also means that R4C4 cannot enter that region
because it would create a smaller loop, and therefore, it needs to escape via
the region with R3C1. We now know both of the visits to that region, and we
need to touch the sun in it, and there's only one way that can happen.
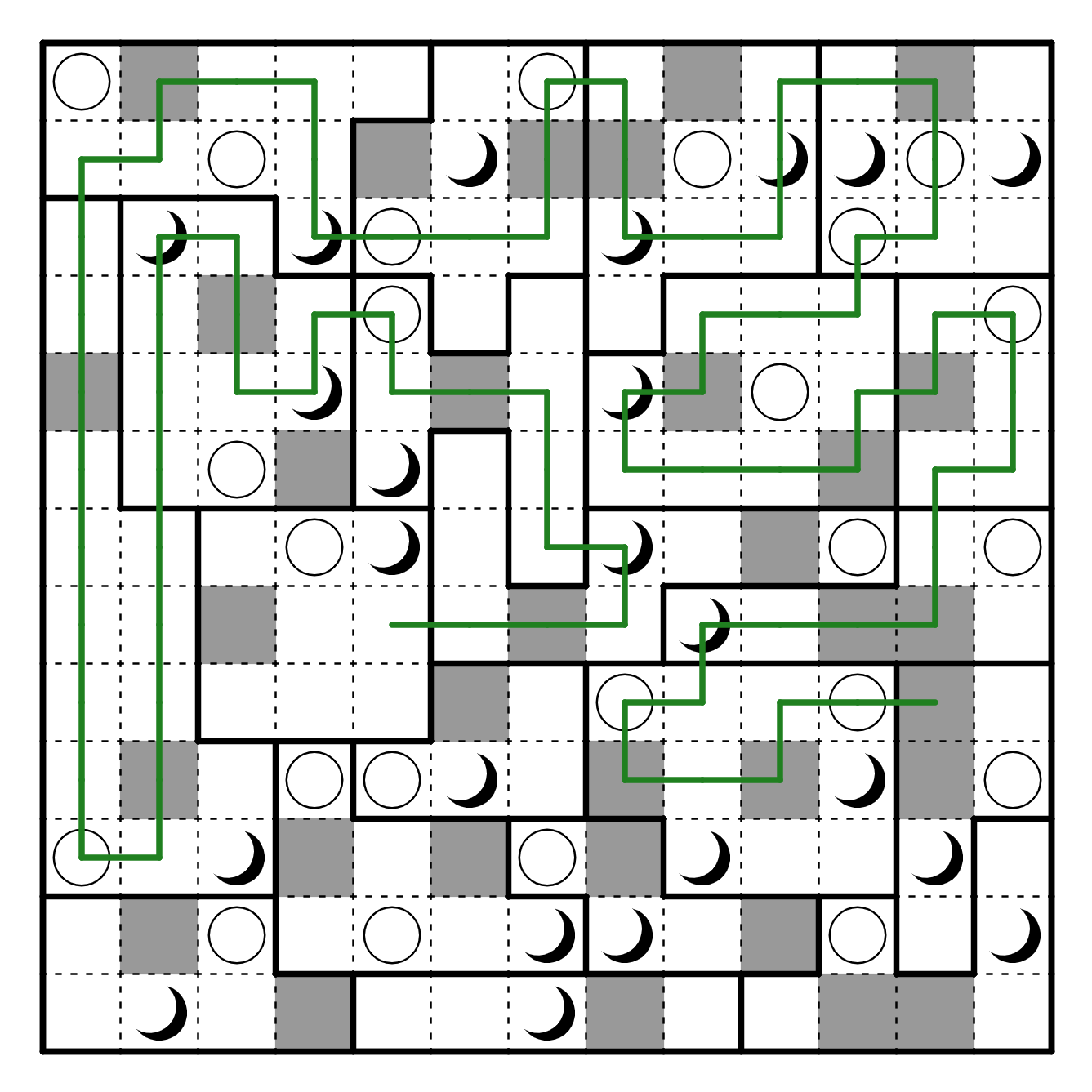
R8C5 needs to visit a moon next, so it must exit via R9C5-6. In addition,
R11C2 cannot be visited in the loop, so it must visit R10C3 and we can
resolve that section as well as the section containing R10C4.
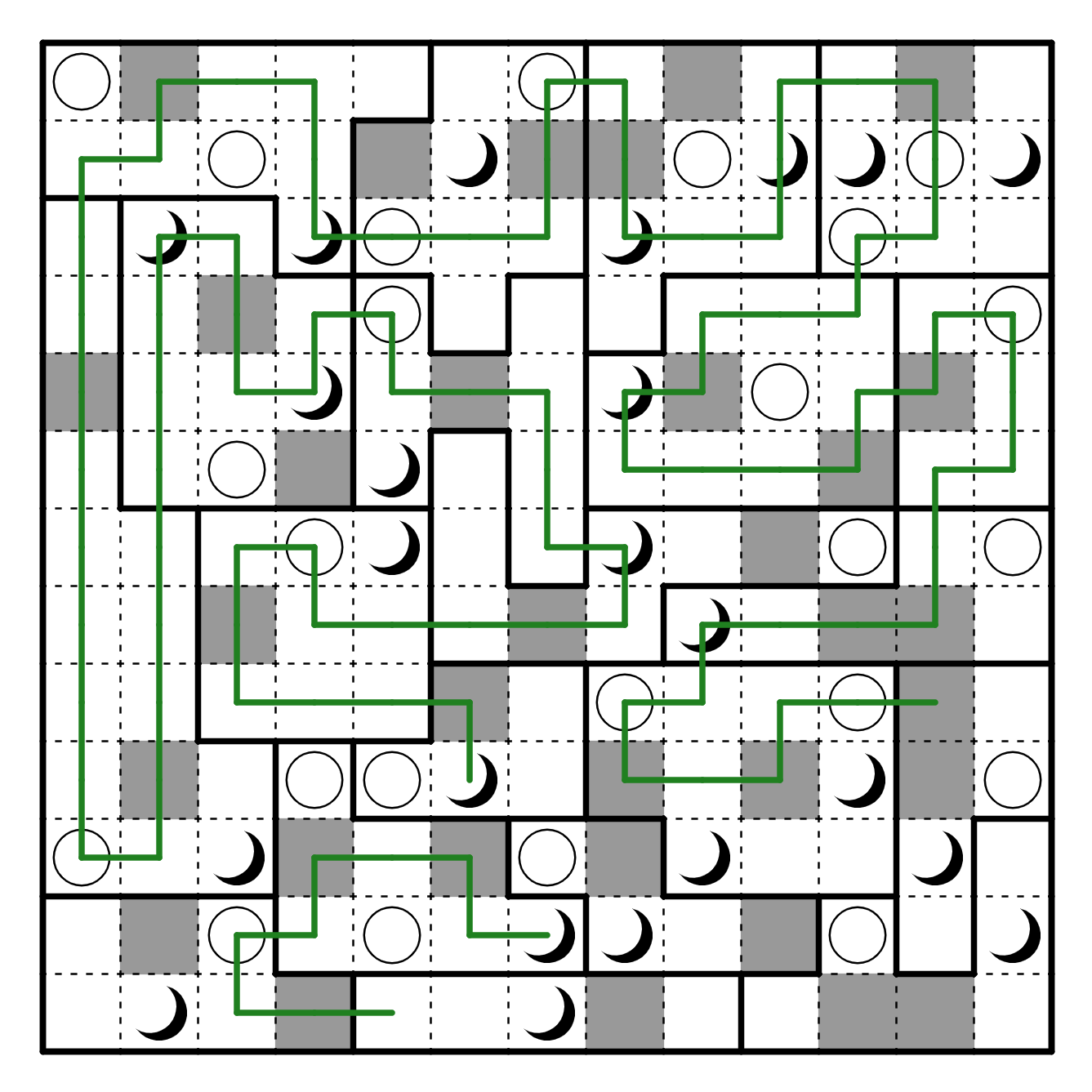
From here, the rest of the puzzle easily resolves:
