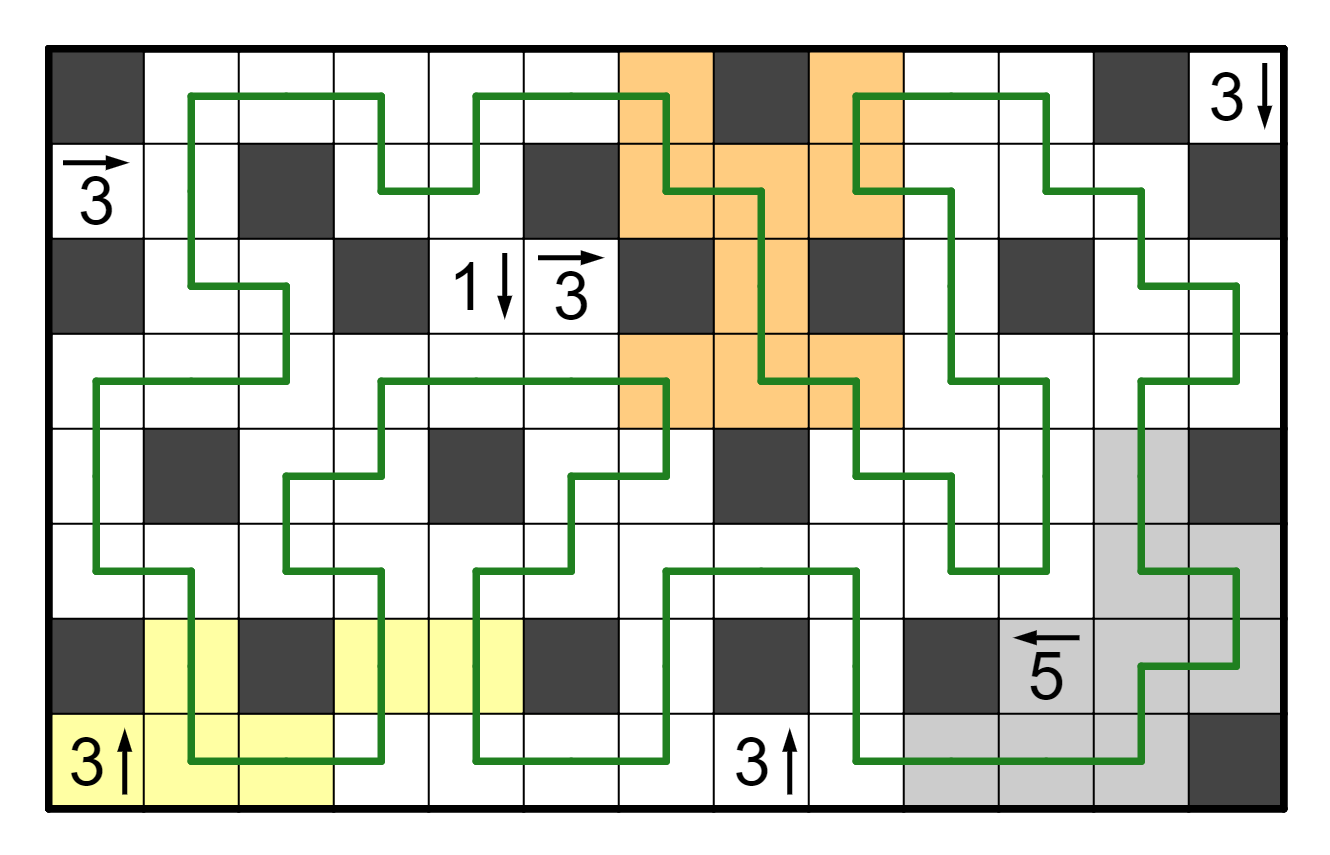
First, solve the logic puzzles. There are nine of them, and in each
puzzle the name of the genre is given, perhaps with rules, but in some
of the puzzles you have to look up the rules separately. A full
solution to all nine puzzles is in the appendix.
Then, there are several observations to make simultaneously. There
are several colored regions in each grid. However, only three of the
puzzles (LITS, Simple Loop, Star Battle) tell you how to extract
from the colored regions. Thankfully, one of these puzzles is a shading
puzzle, one is a loop drawing puzzle, and one is an object placement
puzzle. Because all nine puzzles fall into one of these three
categories, it makes sense to apply the same type of extraction to the
other puzzles of each category.
The key idea of this puzzle is that we are creating a purist/rebel
alignment chart of these nine logic puzzles. The flavortext clues this
with the words "rebel" and "alignment", as well as providing the two
axes, and the title of the puzzle loosely hints towards this as well,
because purist/rebel alignment charts are questioning what a title is.
See the
sandwich alignment chart
for an example of this.
The flavor states that the speaker is "down" for "any grid shape",
implying that the three puzzles with the weird grid shapes (Nurikabe,
Simple Loop, Tents) are the bottom row of the grid. Similarly, they
think not including the rules is "right", so the puzzles that only
state the name of the genre (Akari, Masyu, Nurikabe) are on the
right column. We can then infer that the top row consists of square
grids while the middle row is rectangular grids, and that the left
column consists of rules featuring extraction while the middle column
does not have extraction. Thus, we can place the nine genres as follows:
| Rules Purist | Rules Neutral | Rules Rebel | |
|---|---|---|---|
| Grid Purist | Star Battle | Uso-One | Masyu |
| Grid Neutral | LITS | Yajilin | Akari |
| Grid Rebel | Simple Loop | Tents | Nurikabe |
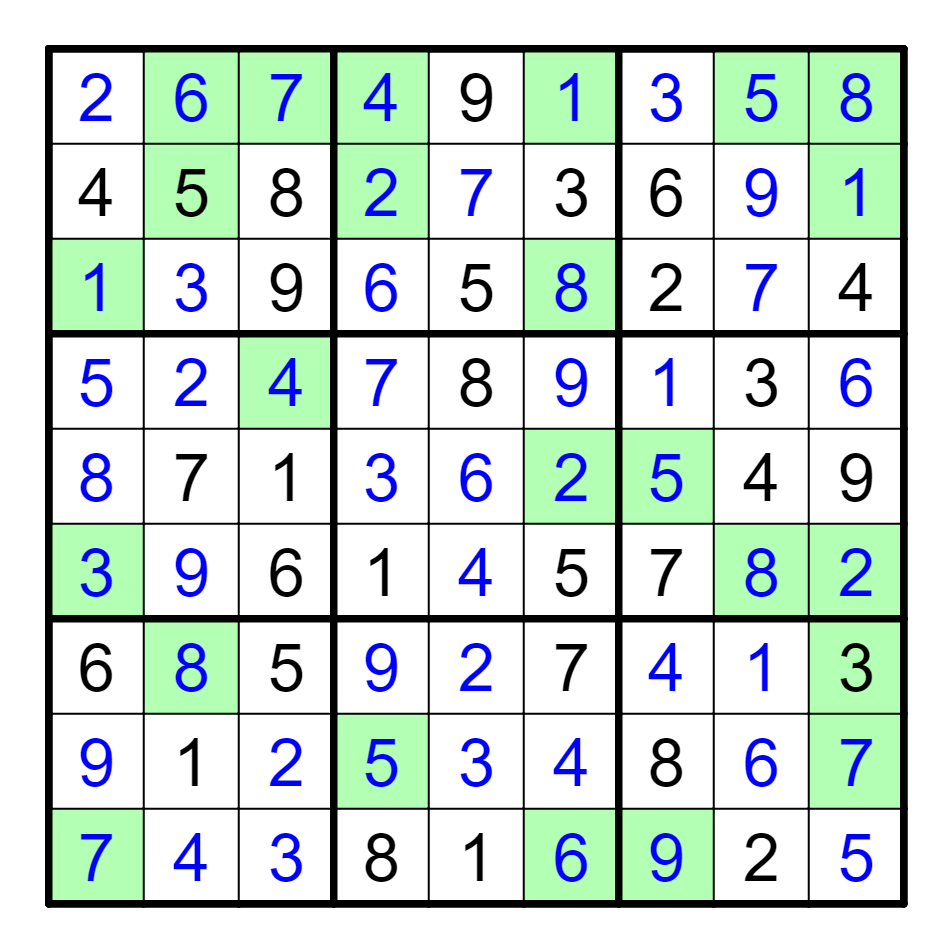
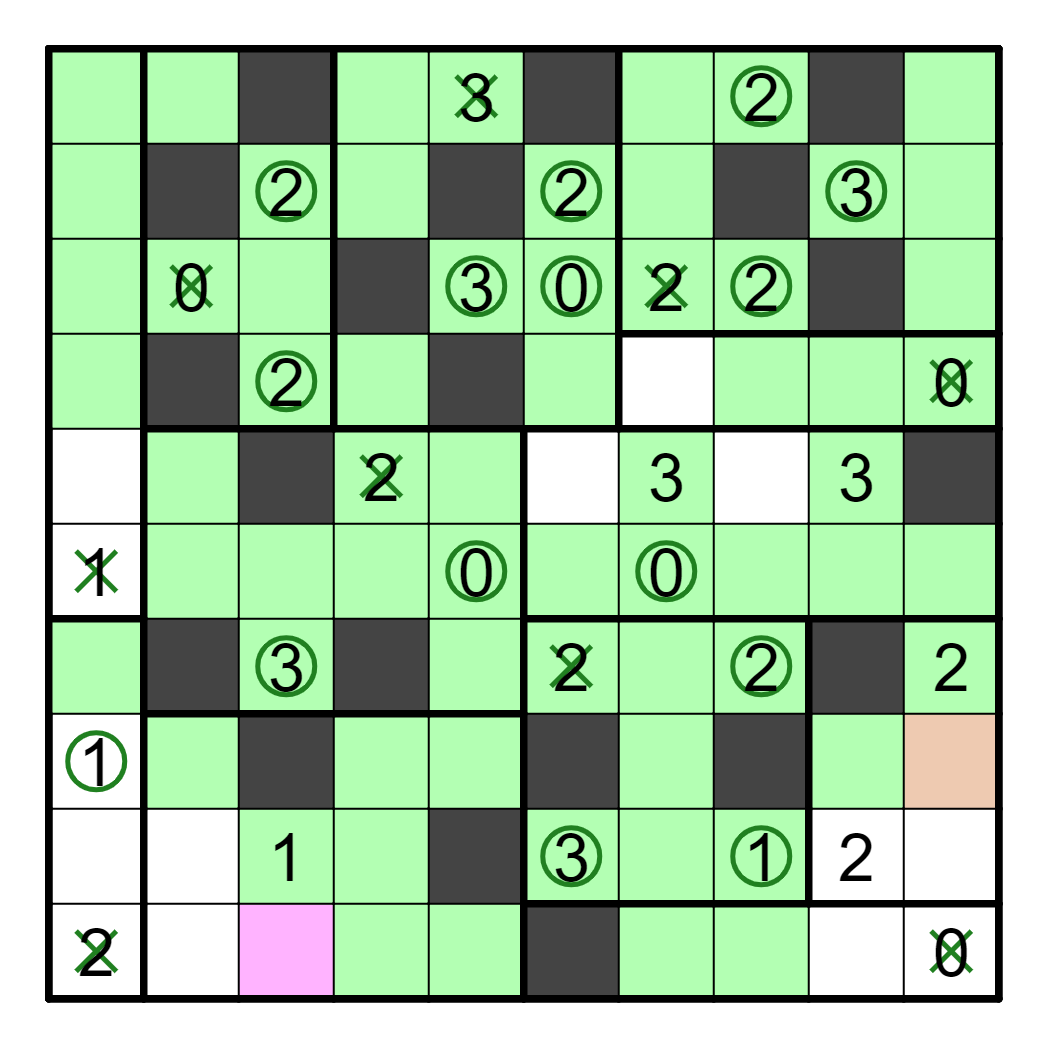
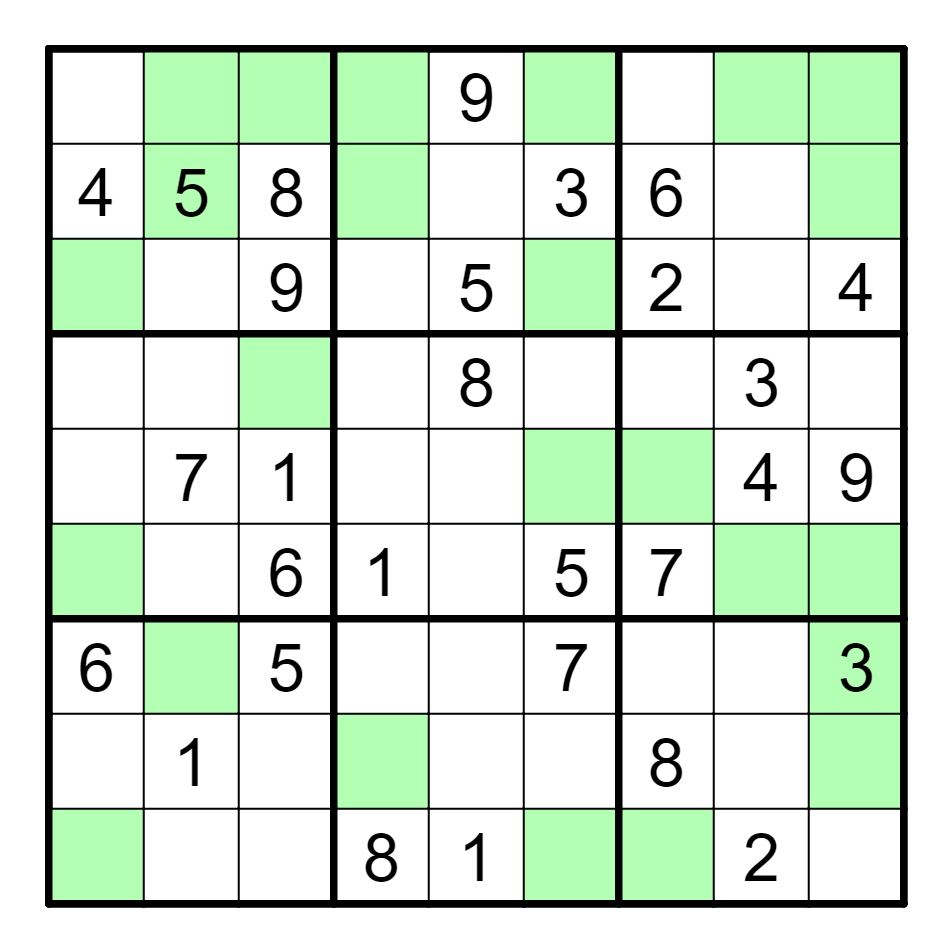
Upon doing this, the puzzle looks like this. This looks remarkably like a Sudoku; indeed, it solves logically as one. Taking the green cells in each box and summing them up, then converting these numbers to letters via A1Z26 yields the answer, SONGBOOKS.
Author's Notes
So this puzzle is... a bit of a marathon. I tried to make the feeders easy while still being interesting, although I think the logic is still a little tricky if you're not already familiar with the genres. Six out of the nine puzzles were nerfed from the original version of this puzzle. If you're not logicked out, here are these original puzzles: LITS Simple Loop Star Battle Tents Uso-One Yajilin
Appendix: Logical Walkthrough
Throughout these solutions, we use RxCy to refer to a cell in a rectangular grid; R1C1 is the top left cell.
Akari
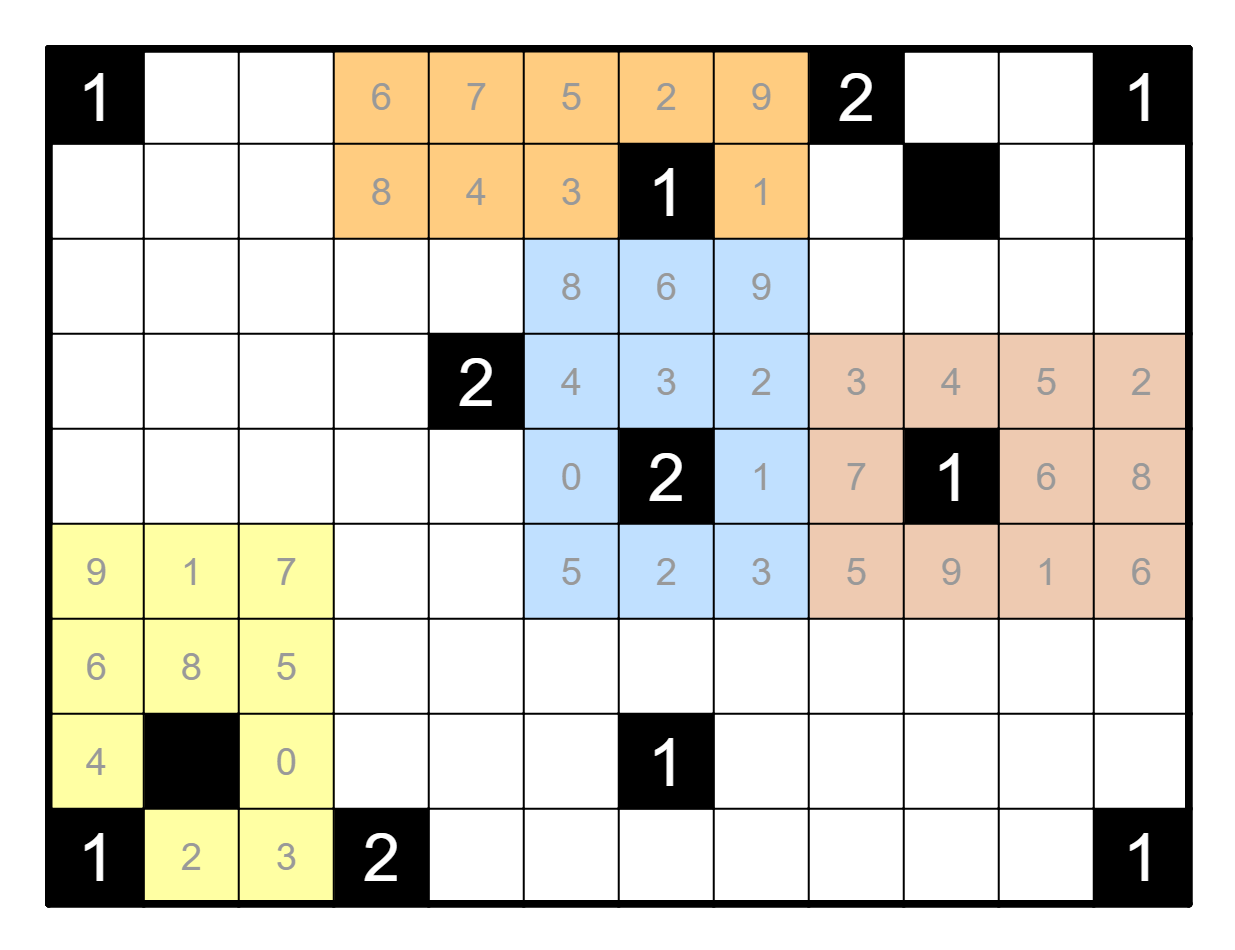
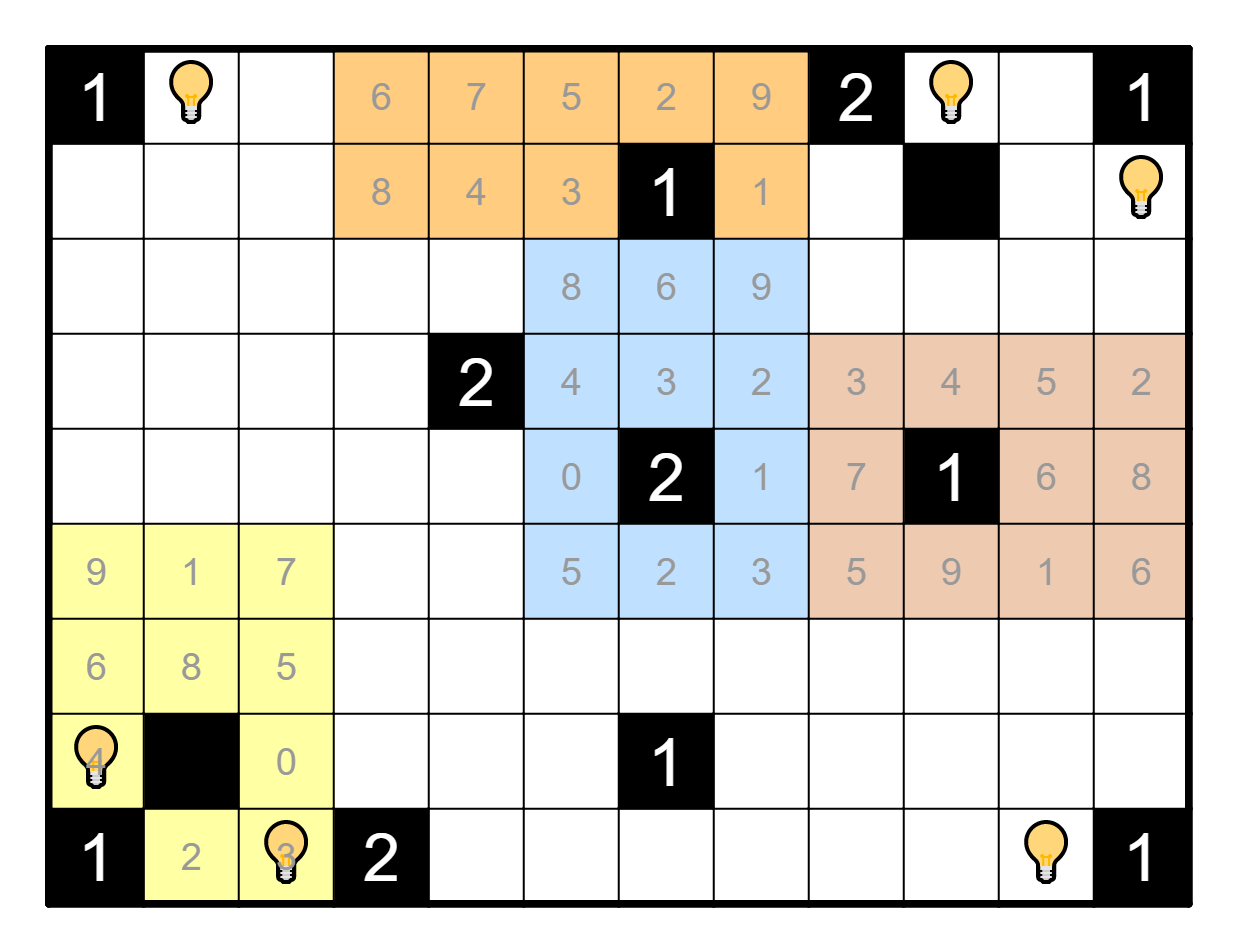
The initial break-in of this puzzle is the outside border. Observe that
there can be at most six light bulbs among the outside border, because
every line in this image can contain at most one light bulb:
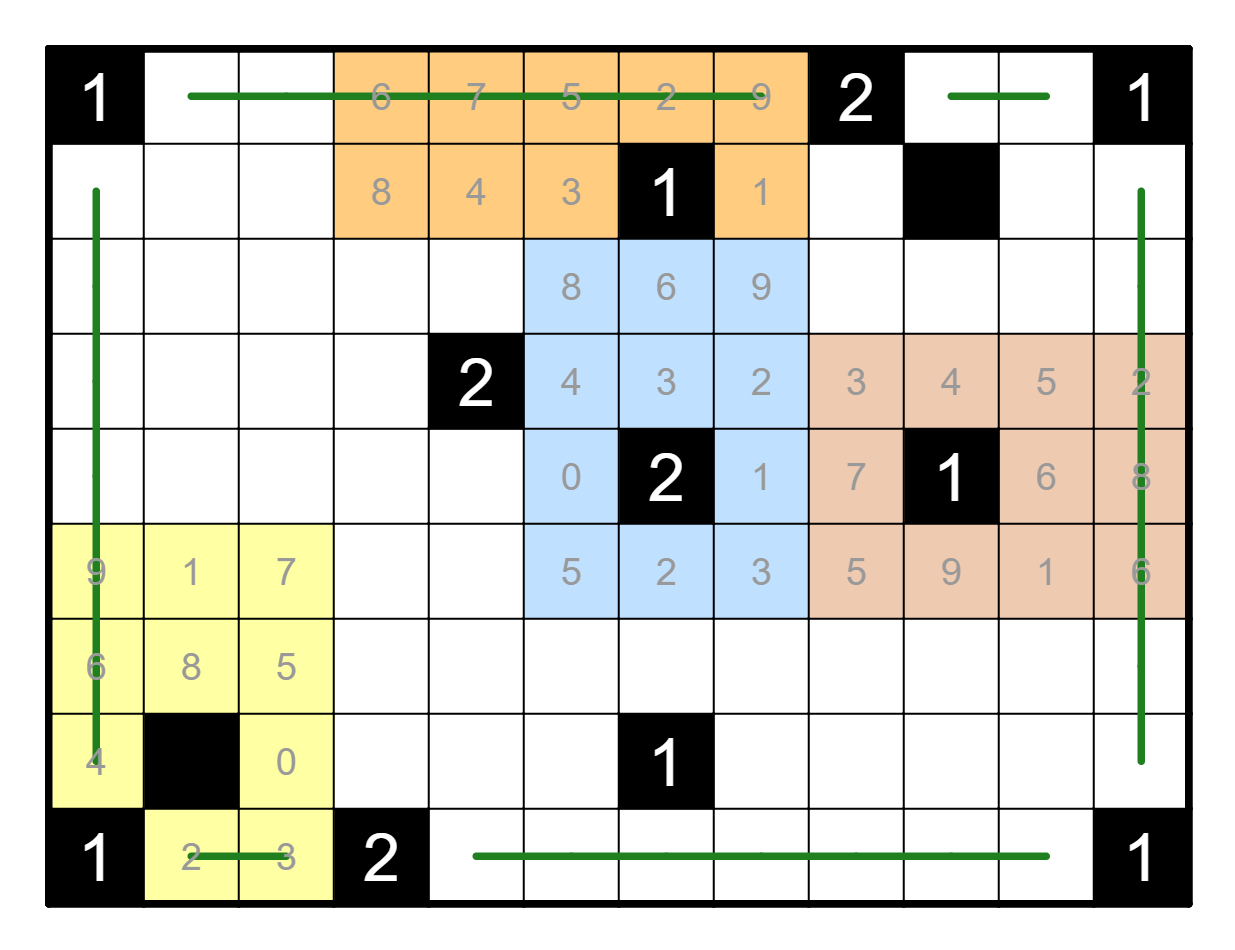
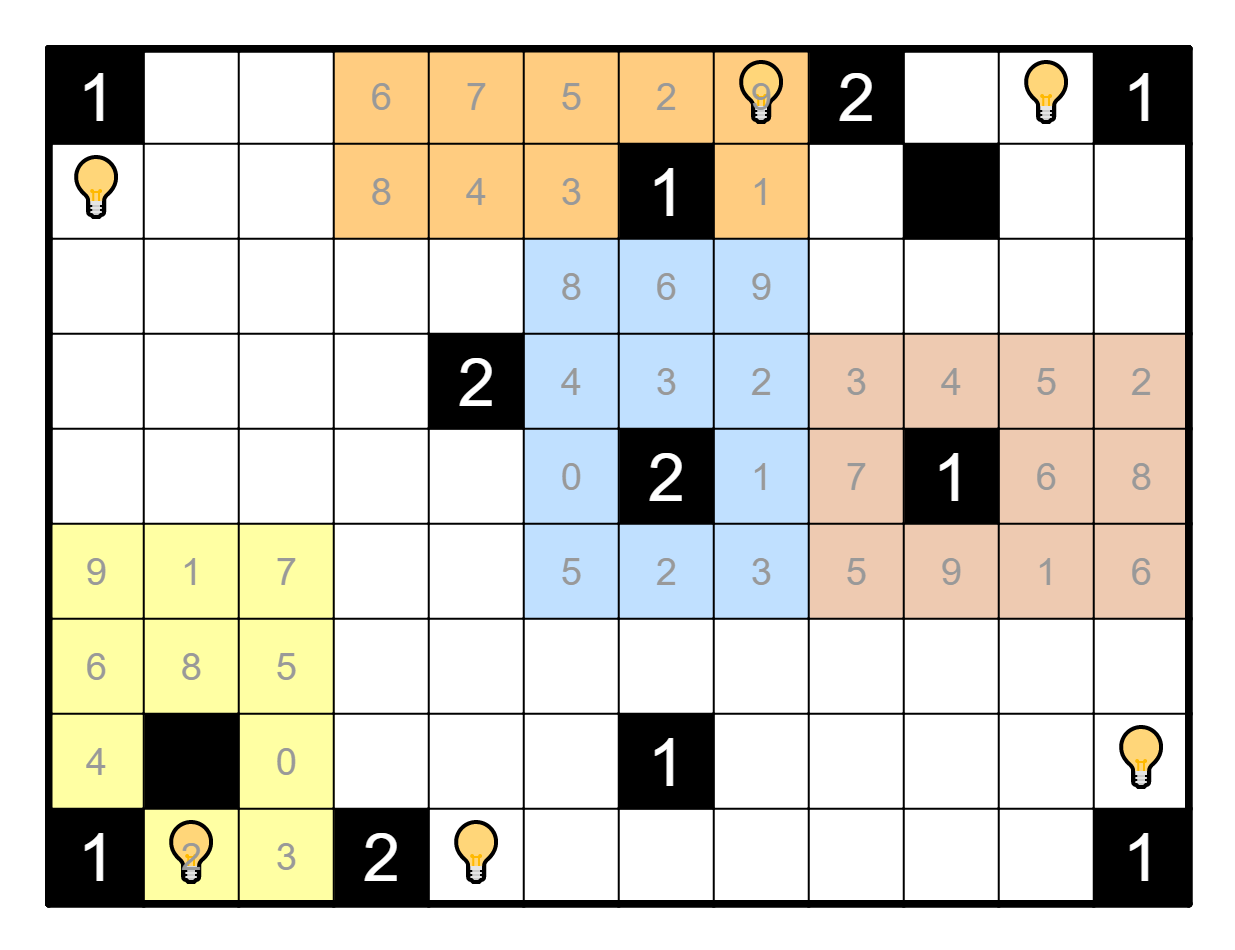
However, consider each of the clues on the outside border (R1C1, R1C9,
etc.) Each of these places a bound upon the minimum number of
light bulbs around it. In this image, each of the clues has at least
one of the pictured light bulbs around it:
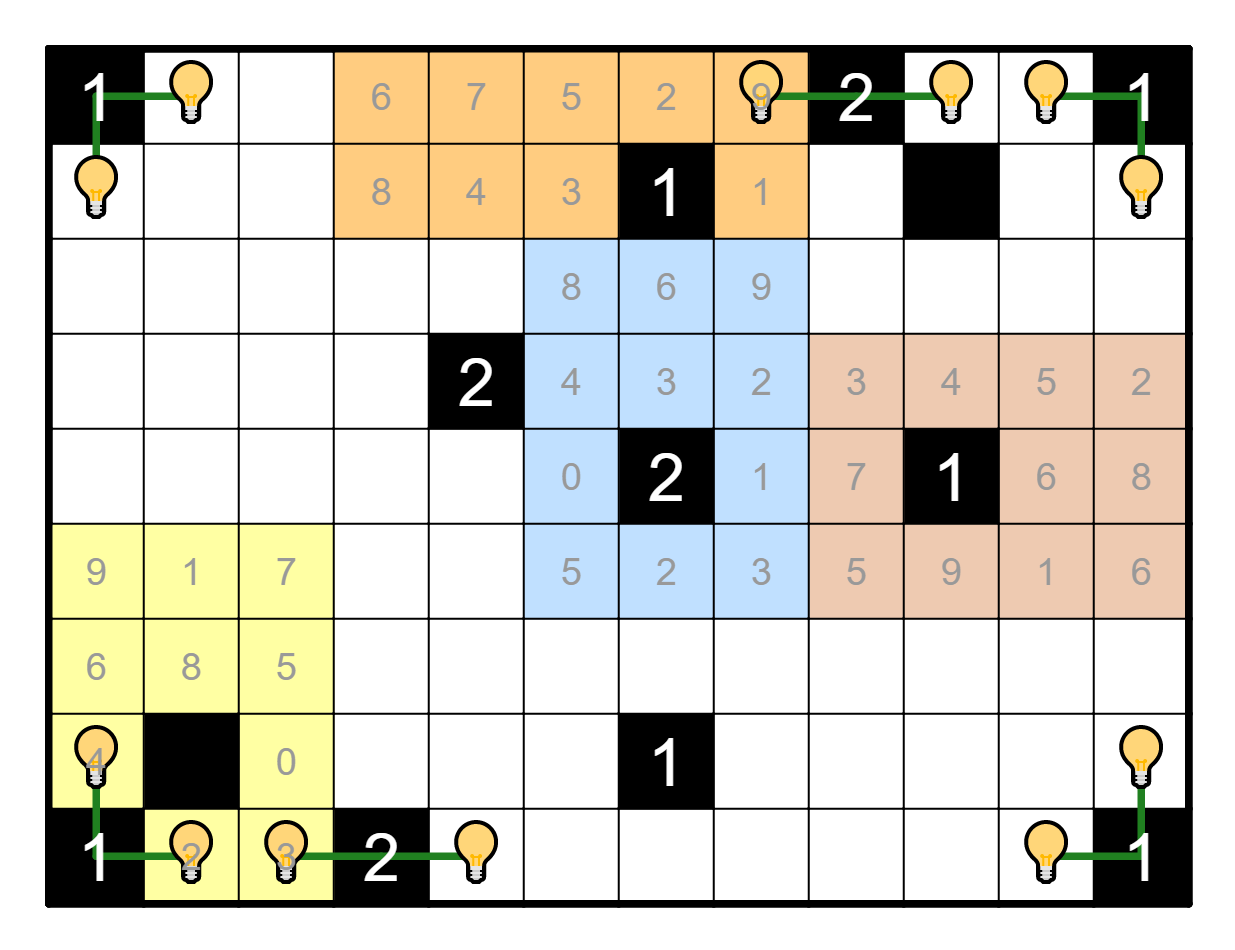
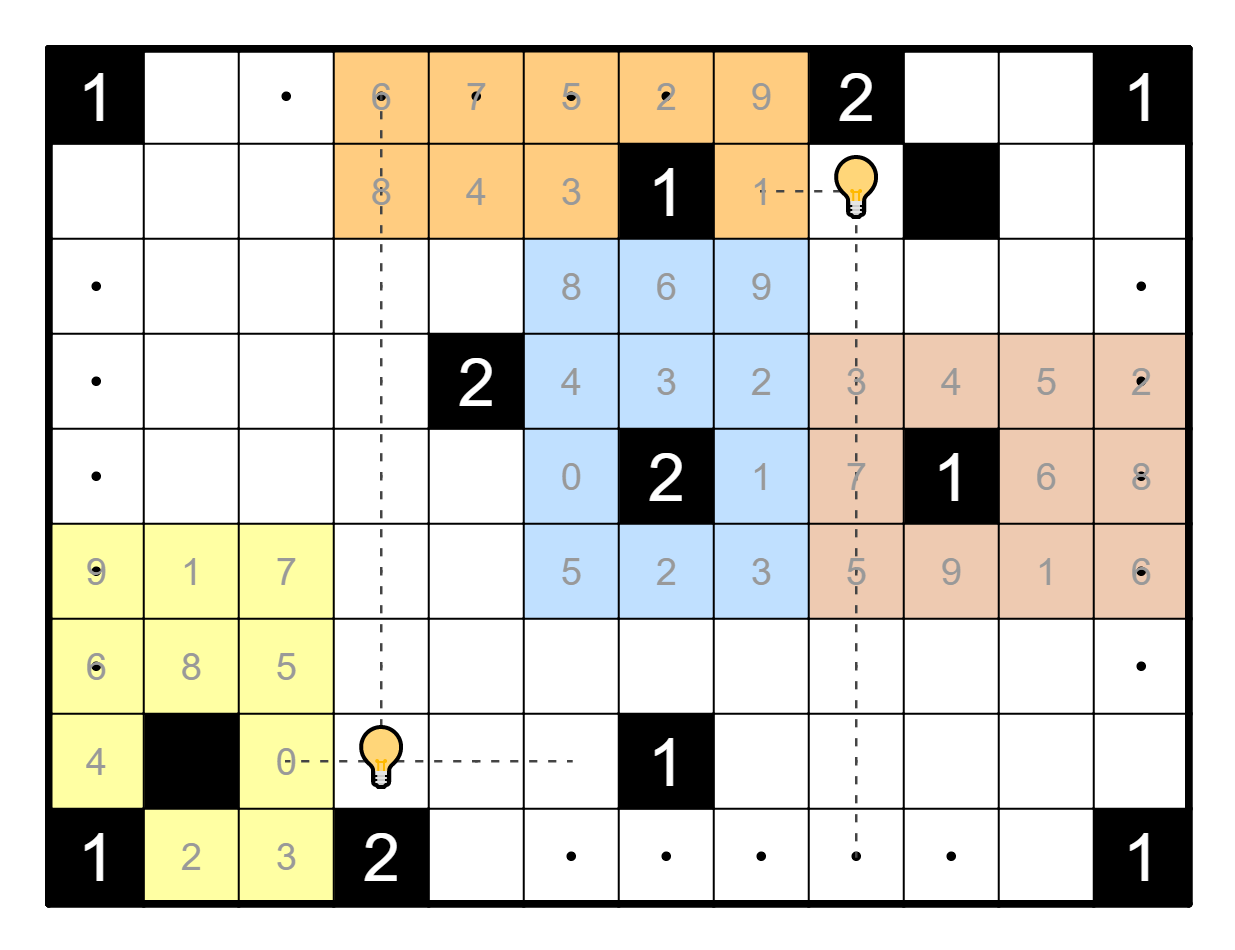
But this makes a minimum of six light bulbs! Therefore, this minimum
must be attained. This means that the outside border only has two
options to take, that can be thought of as a clockwise circle or a
counterclockwise circle:
There are two key takeaways from this. First, we know that no
other cell on the outside border can have a light bulb (otherwise
there would be more than six). Second, consider the 2-clues on the
border. They cannot have both of their adjacent border cells have
light bulbs, so the one remaining cell must have a light bulb.
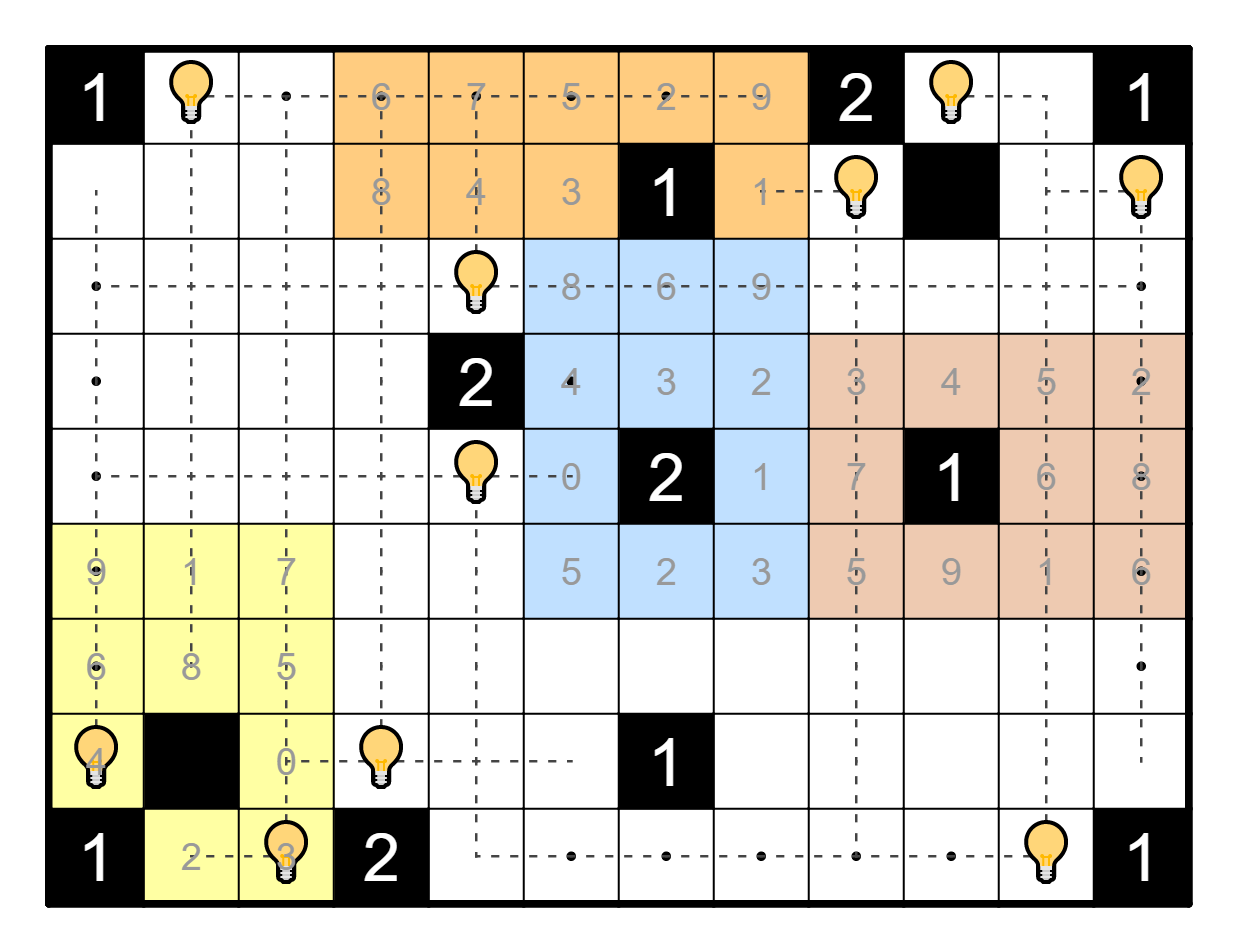
The next observation is to consider the cell R4C6. We claim this cell
cannot have a light bulb. Indeed, if it contains a light bulb, then
the 2-clue in R5C7 is resolved, but this will form a contradiction with
the 1-clue in R8C7, which has no place it can go.
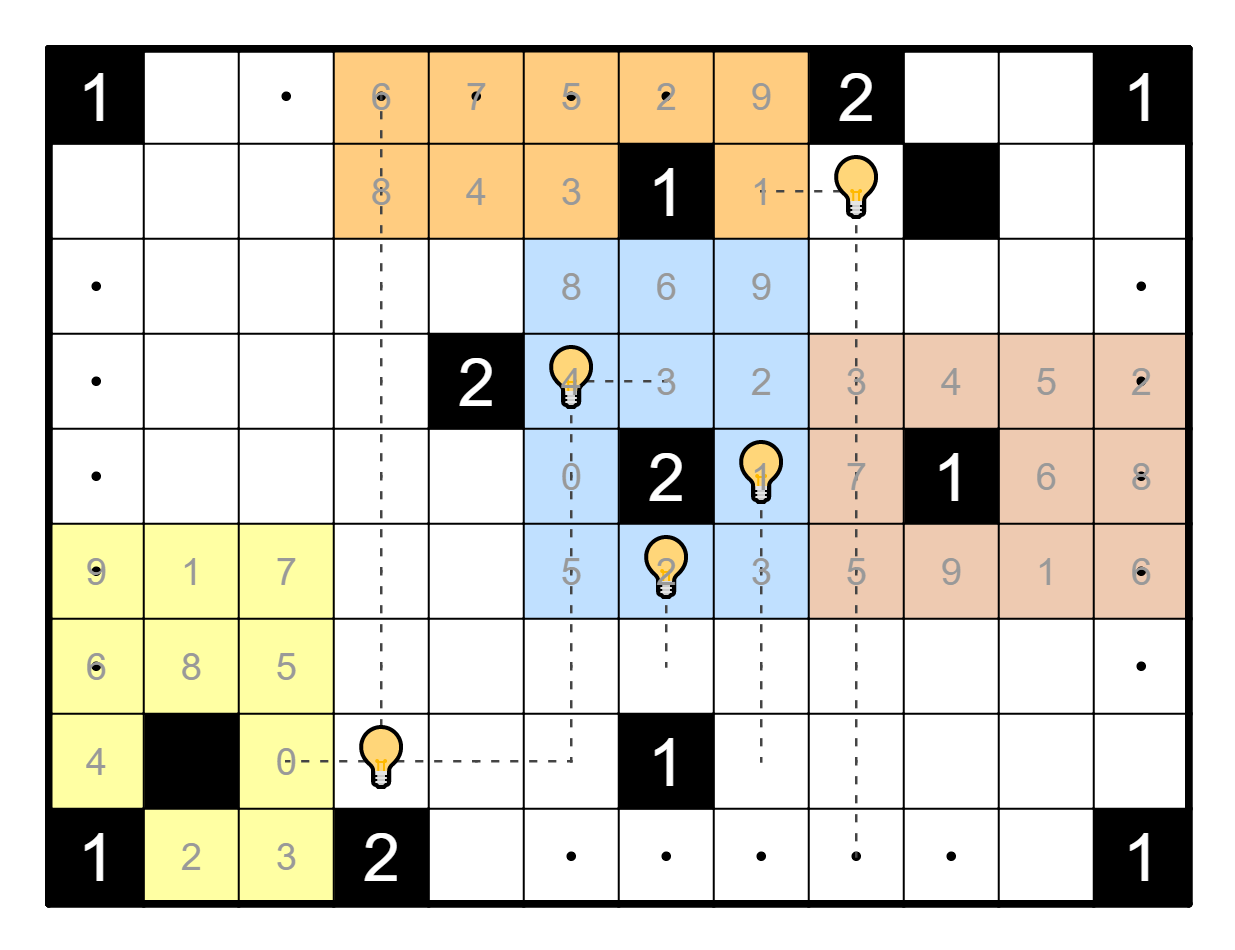
Thus R4C6 cannot have a light bulb, which places light bulbs in R3C5
and R5C5. Because the light bulb in R5C5 sees R9C5, we now know
which of the two border options was correct.
The puzzle is pretty easy to just guess from here (and indeed,
it may be faster in this puzzle to just assume both of the cases
of the border and see which one works), but let's finish the puzzle
logically. R2C6 must have a light bulb because it's the only way to
resolve the 1-clue in R2C7, but also, let's consider what happens if
R4C7 does not have a light bulb. If this is the case, then R5C8 and R6C7
must both have light bulbs to resolve the 2-clue in R5C7, but if this
happens then there's no way to resolve the 1-clue in R8C7.
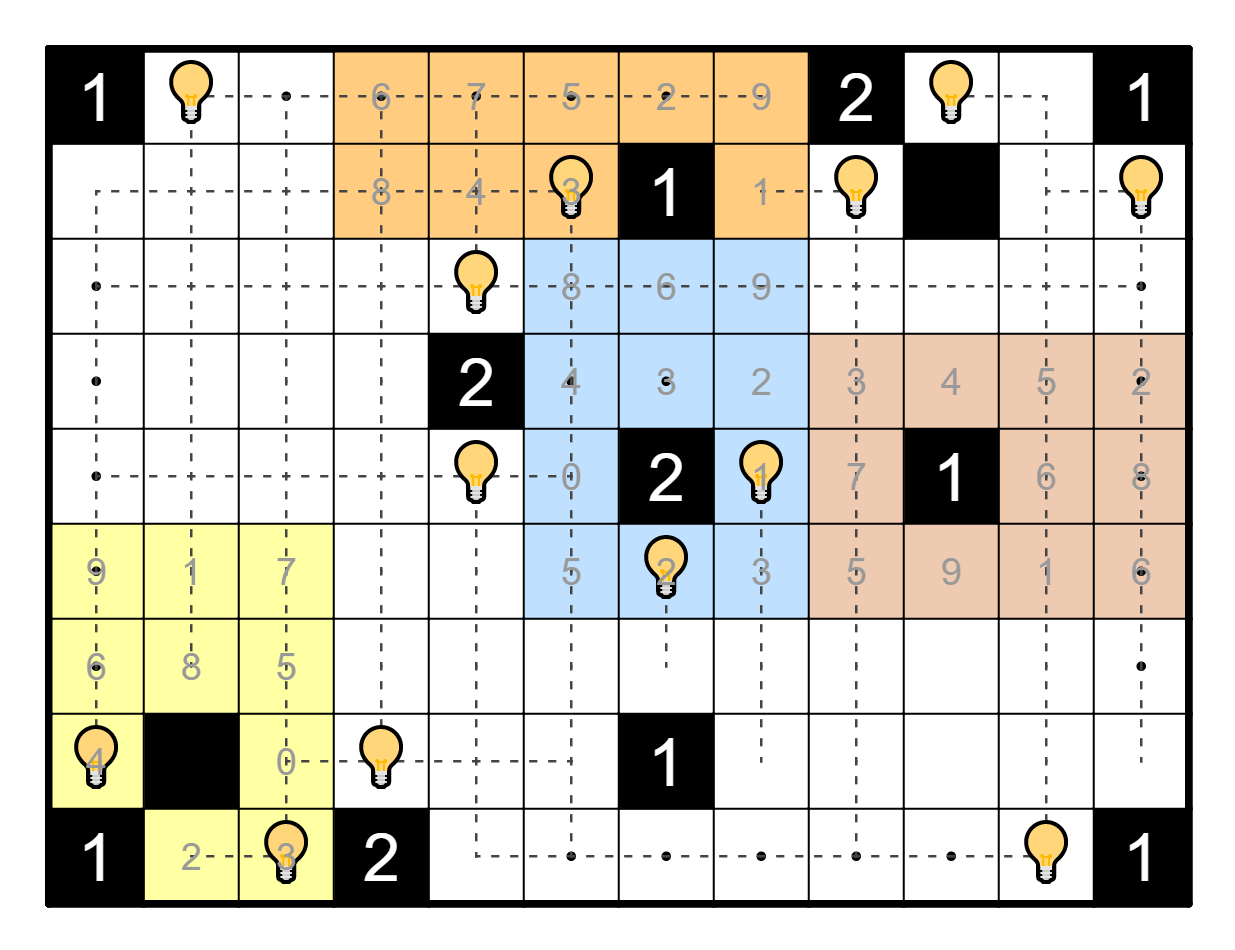
Therefore there must be a light bulb in R4C7. This resolves the 1-clue
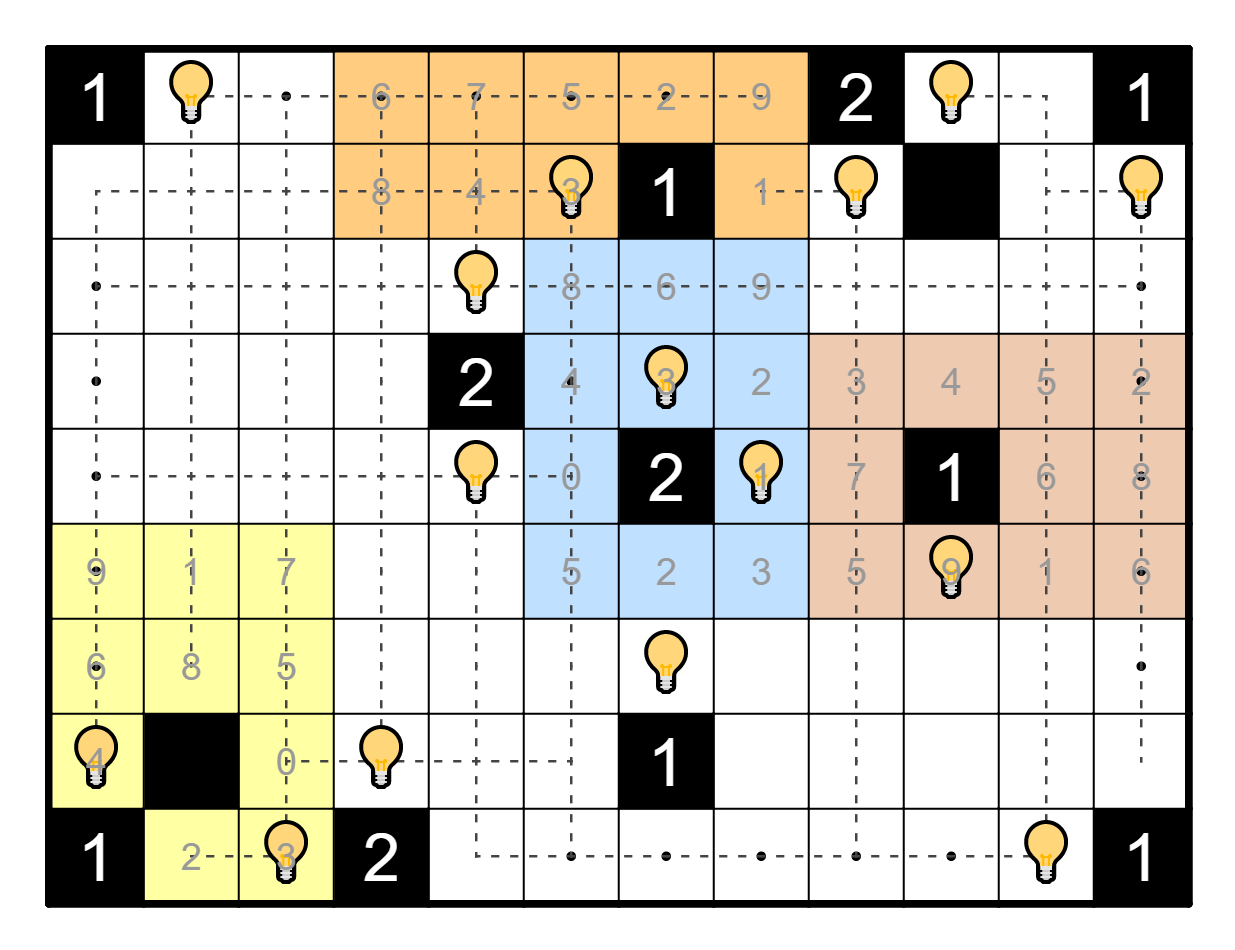
in R5C10, and the rest of the puzzle is finished off quickly.
LITS
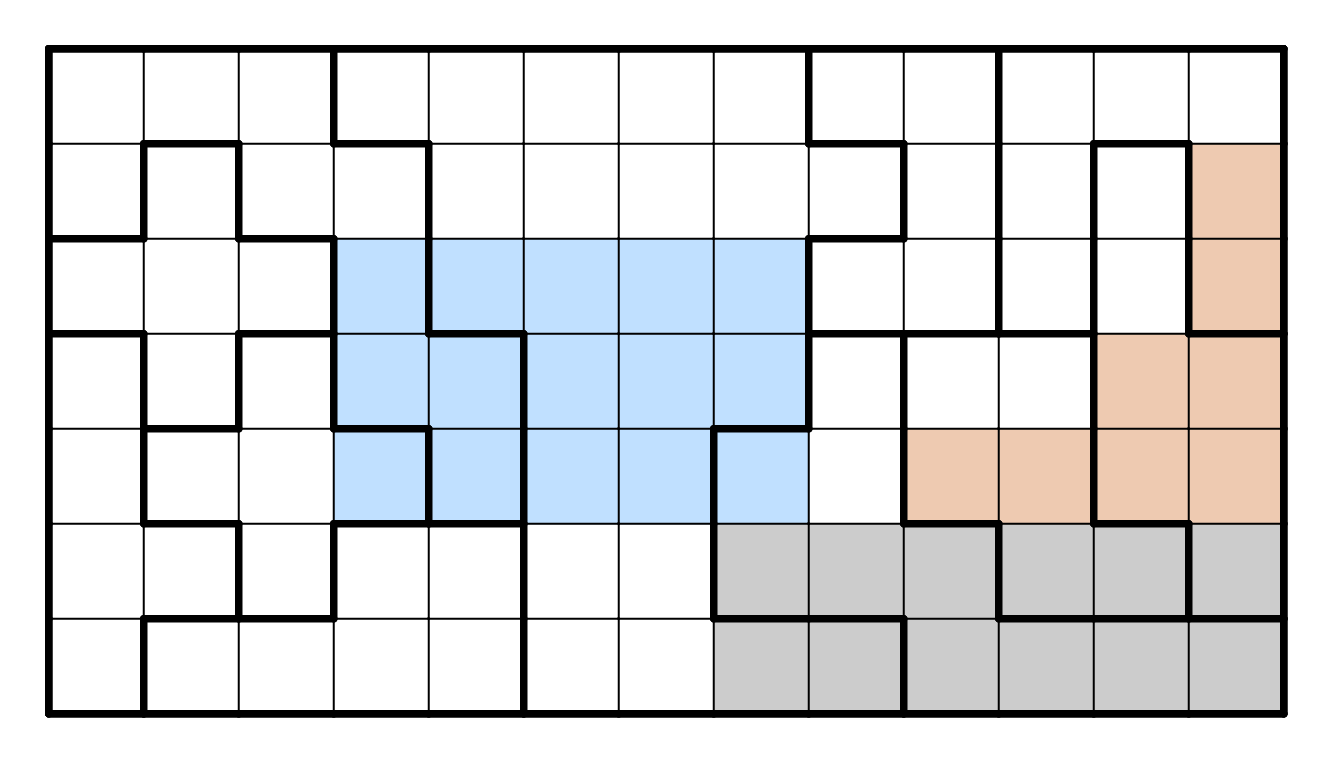
There are two "halves" of this puzzle that are connected at the end.
Let's first try to resolve the left half. First, consider the two
cross-shaped regions. Both of these need to contain a T-tetromino;
there is no other way to resolve them. However, this means that the
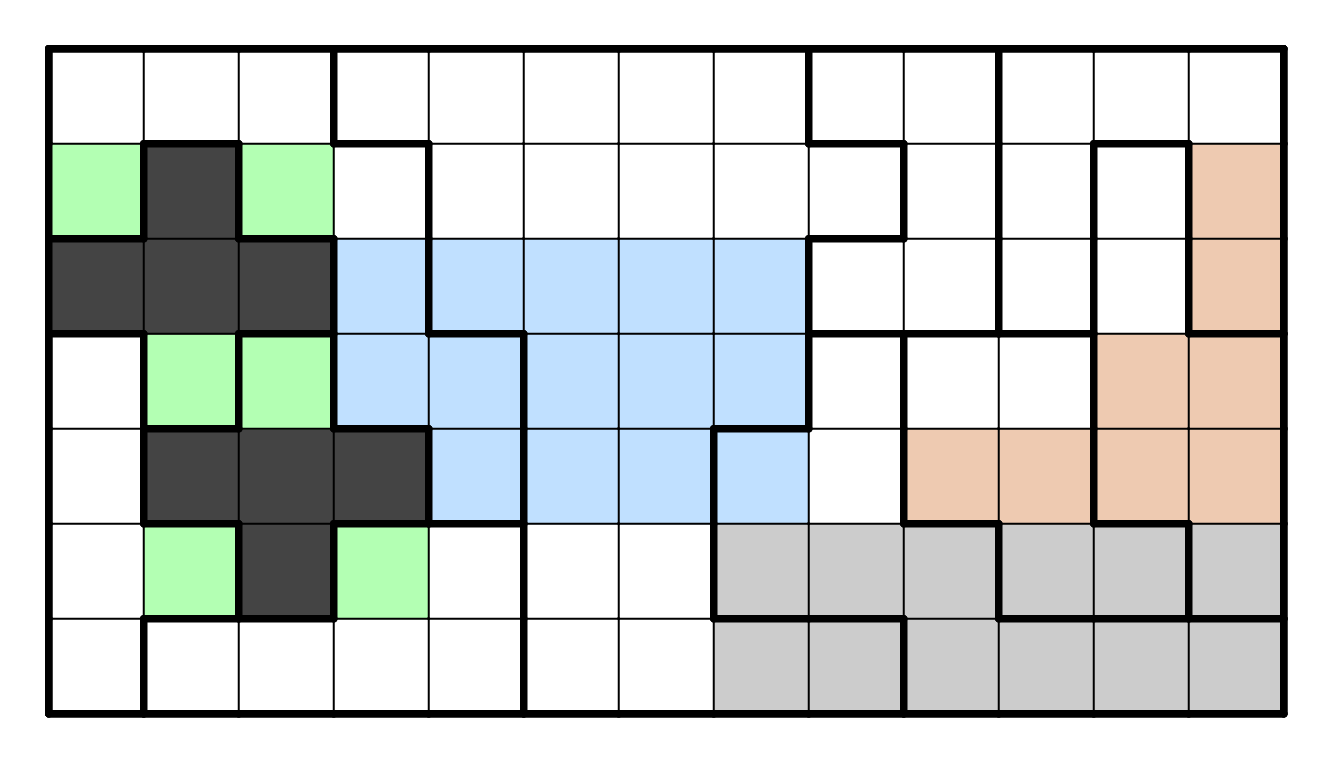
two T-tetrominos cannot touch. It turns out that if R4C2 or R4C3 are
used, then this will always occur, so therefore these cells cannot be
used, and the tetrominos are resolved:
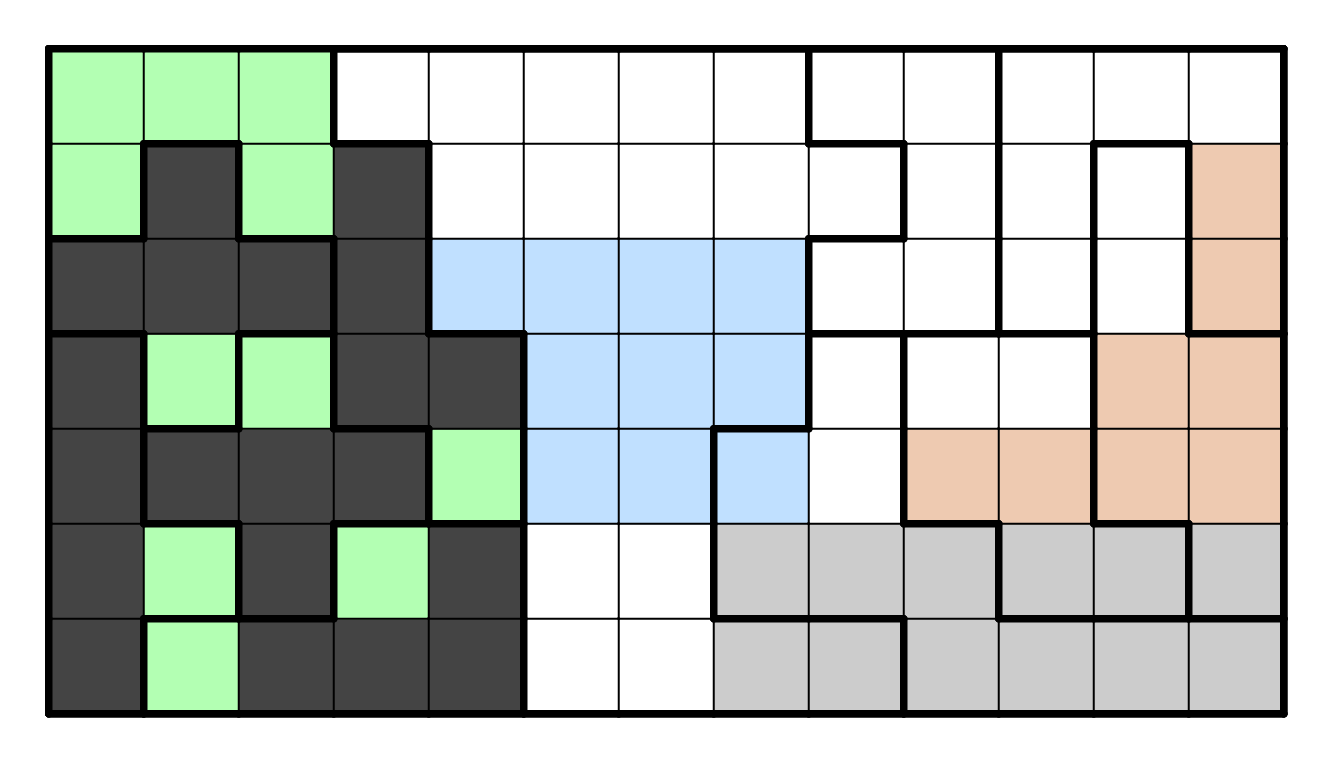
Applying the no 2x2 rule leaves only one option for the bottom left
region, which is an I-tetromino. Afterwards, there are only two
ways to resolve the region next to it, but one of these two ways
makes an I-tetromino that touches the other region, so that region
is also resolved. Finally, considering the top region, R1C1-3 cannot
be used because there are only three cells that do not connect to any
other usable cell. This leaves only two options for that region,
but one of them forms a 2x2 (R45C45), so that region is resolved also.
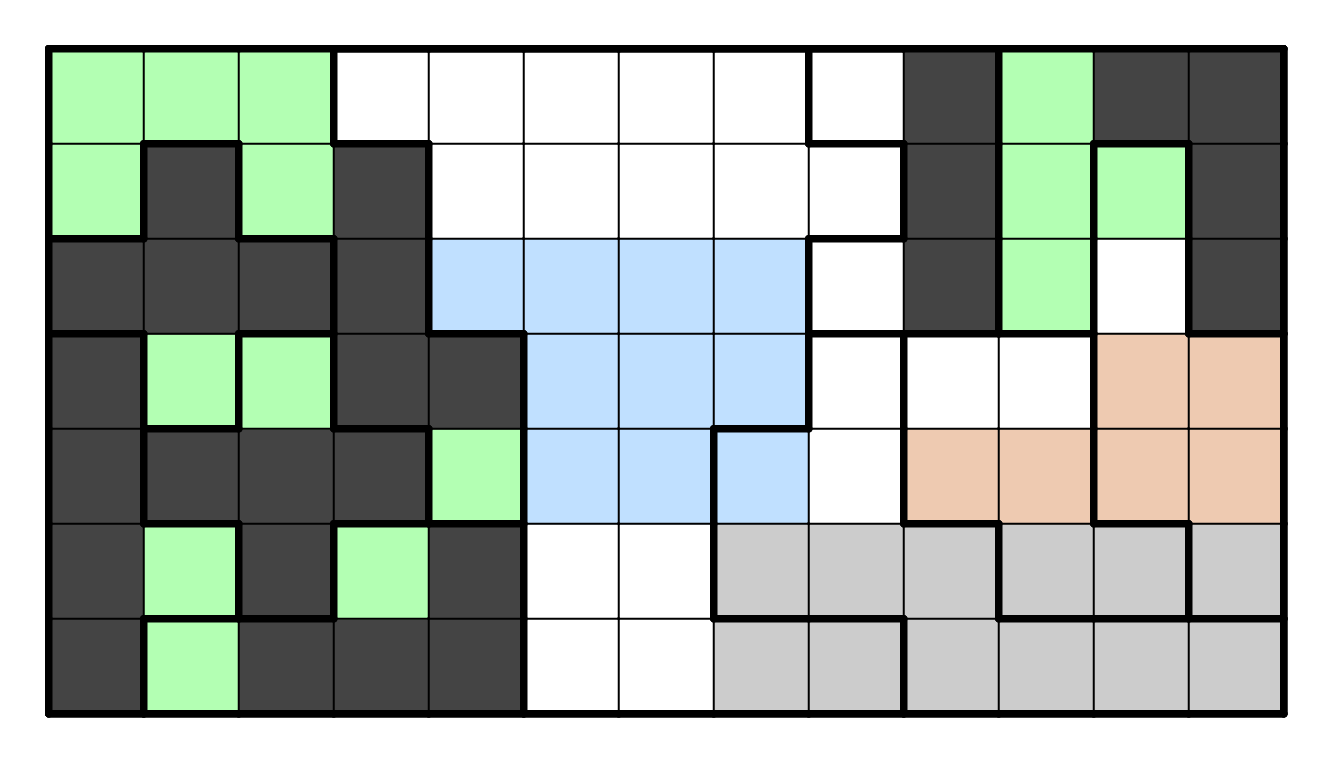
Now, we can turn our attention to the right half. The first step is
to consider the two top regions, especially the one that has five
cells in it. There are only two ways to resolve that region, and
both of these ways form an L-tetromino with cells R1-3C10 shaded, so
we can mark those three cells as shaded. Afterwards, the region next
to it also must form an L-tetromino regardless, so it cannot touch
those three cells, which leaves only one option available.
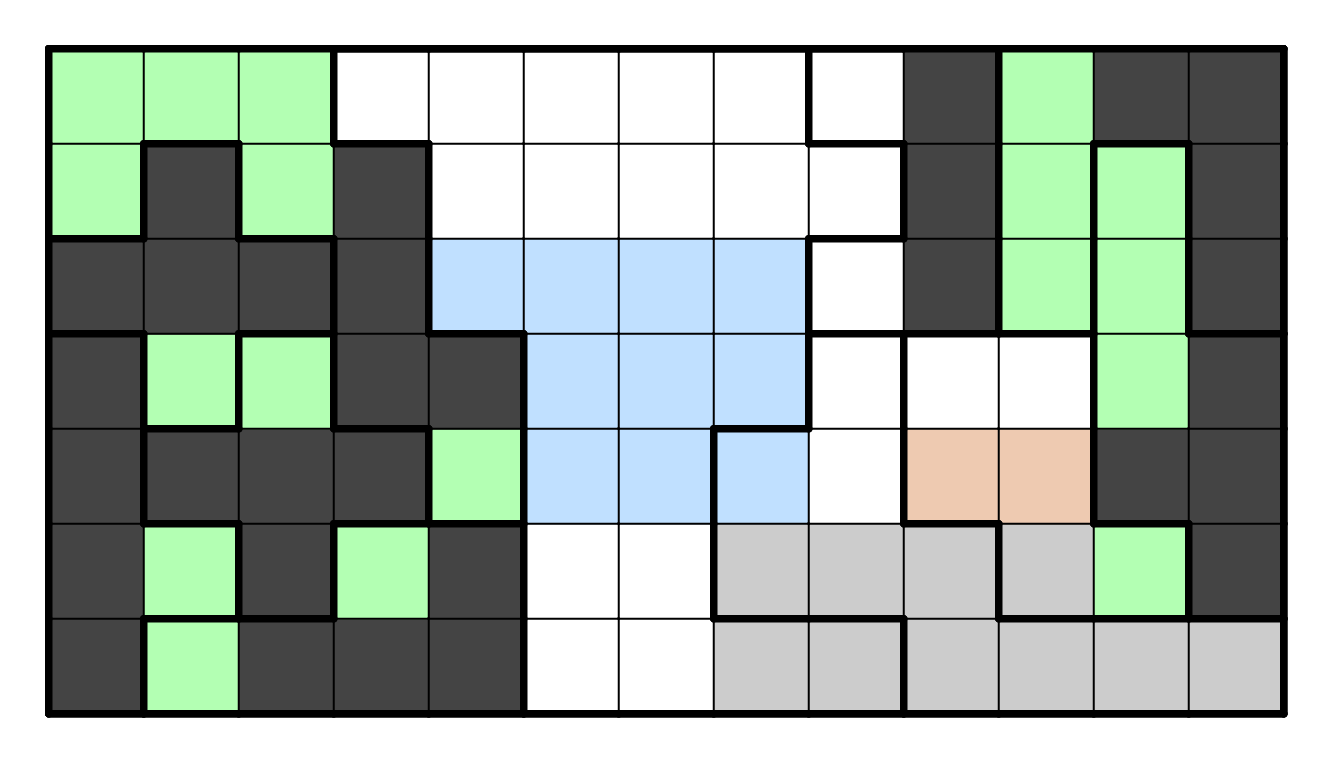
Now, consider the region below the filled-in region (the one in the
middle-right). In particular, we claim R3C12 cannot be shaded. If
this were to happen, the only way to resolve that region that does not
form a 2x2 will make an L-tetromino that touches the one we just filled in.
After this, R4C13 must be shaded because all shaded cells are connected
in the end, and furthermore there is only one way to resolve that
entire region without forming a 2x2 or a touching L-tetromino.
Actually, we can now resolve the region to the left of that T-tetromino
now as well. The cell R6C11 is shaded because not shading it leaves
only four cells in that region which form a 2x2, which in turn shades
R5C11. Afterwards, we must avoid a T-tetromino because this touches one,
but also, if we were to form an L-tetromino in this region (with cells
R4C10 and R4C11), then this would touch the above five-cell region which
we established at the beginning of the puzzle must contain an L-tetromino.
This leaves only one option for this region, forming an S-tetromino.
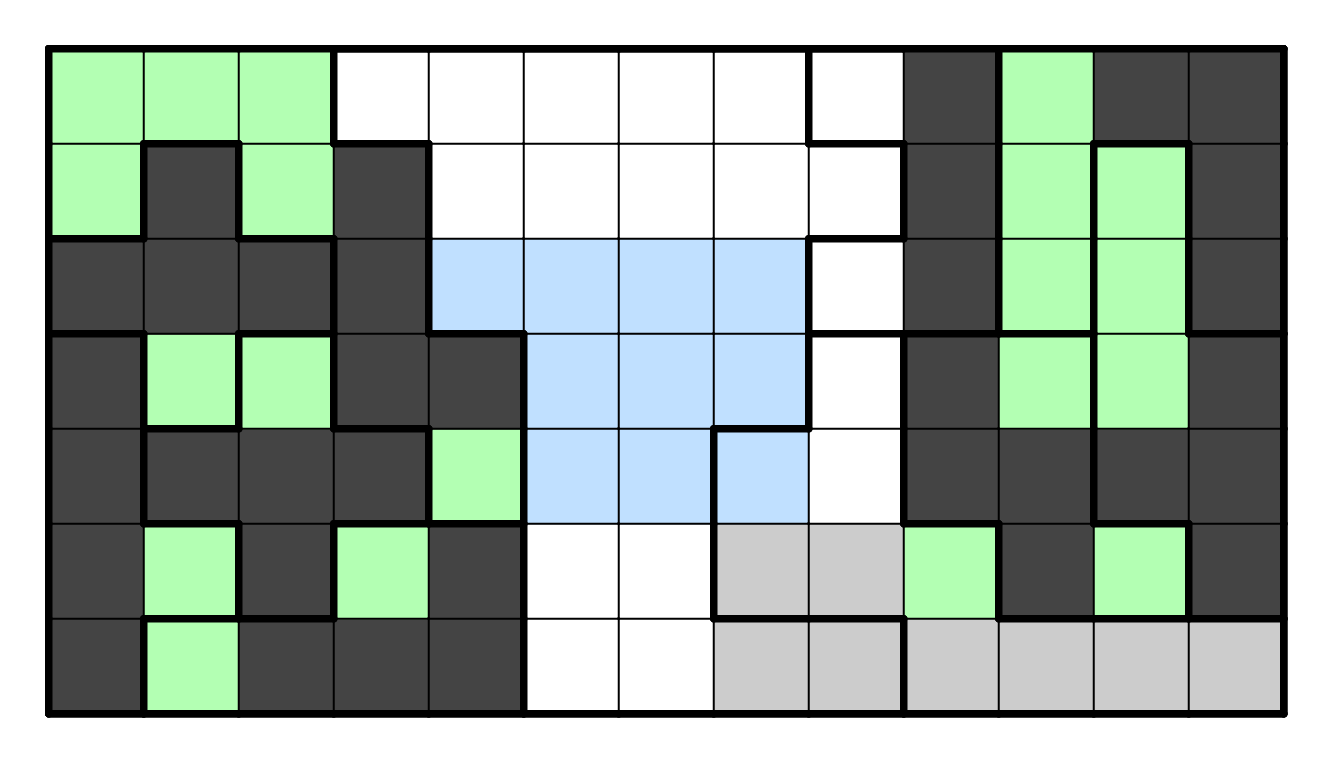
Consider the region below and left of this S-tetromino region. There are now
only two options for where the tetromino can go. However, if it goes to the
left, there is no way to place it that does not form a 2x2 tetromino; either
you take both cells R4C9 and R5C9, or you form a 2x2 in that region itself.
Therefore that region is resolved fully.
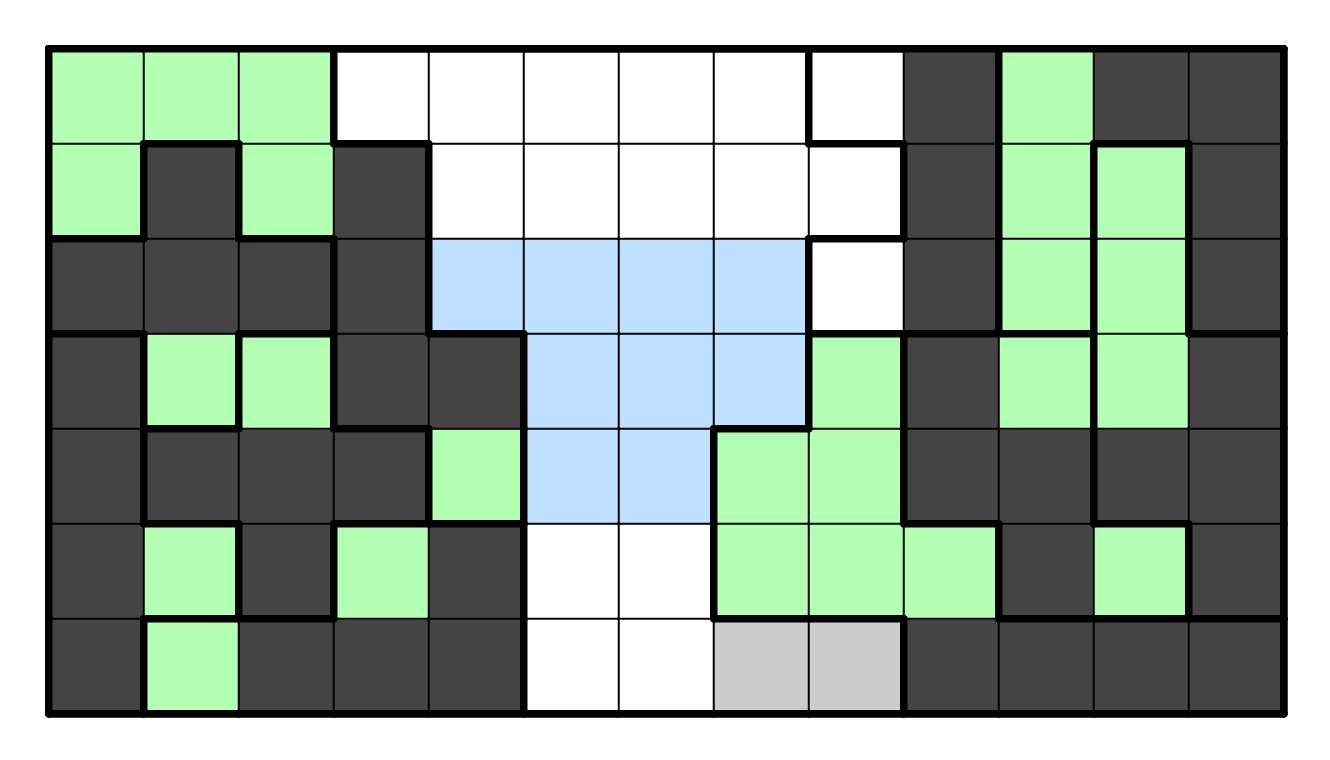
Now, we need to consider how to connect the two sides to satisfy
connectivity. If we do not use the L-tetromino at the top, then we could
connect via the bottom, but this requires two I-tetrominos to touch.
So, we need to use the L-tetromino, and if we were to use R1C9, then
no two cells from opposite sides are close enough. This forces
R3C9 to be shaded, after which there is still only one way to resolve
the connection that does not form a 2x2 or force two L-tetrominos to
touch each other.
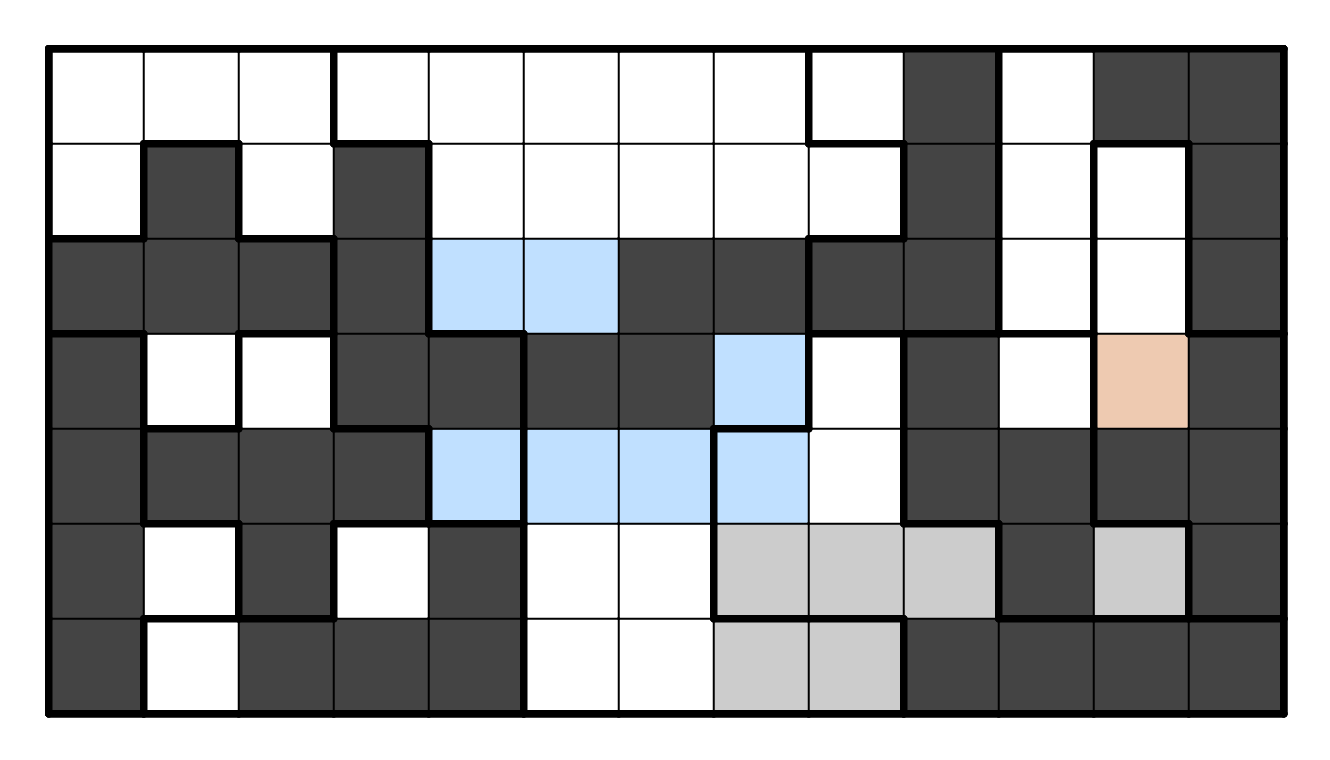
Masyu
We can start this puzzle off by drawing some "trivial" lines.
If a black pearl is too close to the edge, then there must be a line
coming out of it in the opposite direction. In addition, a white pearl
on the edge must be passed parallel to the edge so it does not go into
the edge of the grid.
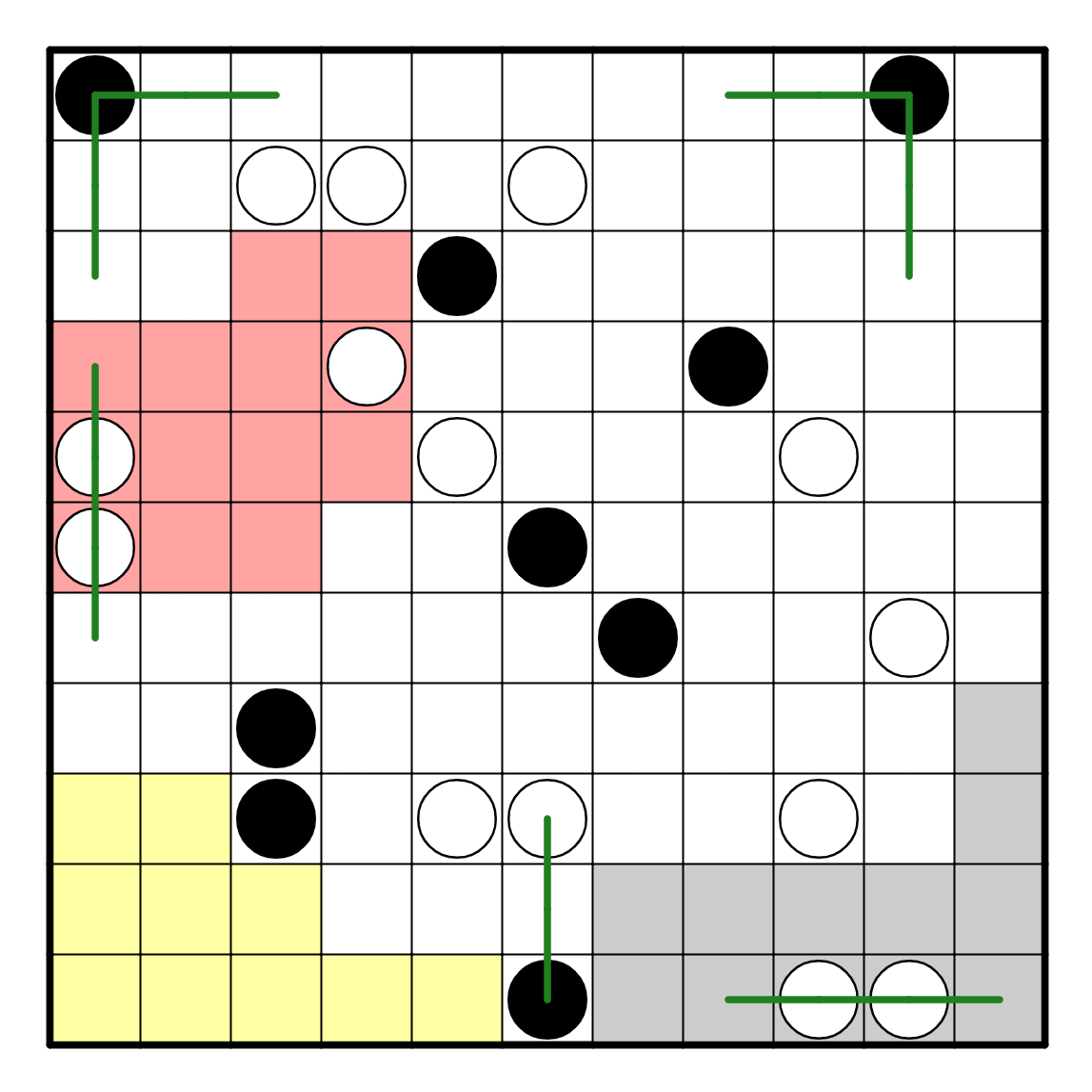
We can apply white pearl rules a few times on the border cells now,
as well as on R9C6. In addition, the two adjacent black pearls at the
bottom left must not be connected directly, because it isn't possible
to let both of them continue to go straight. Then, the bottom one of
this pair must also turn left because if it turned right it would
cross the white pearls and intersect at R9C6, which is a problem.
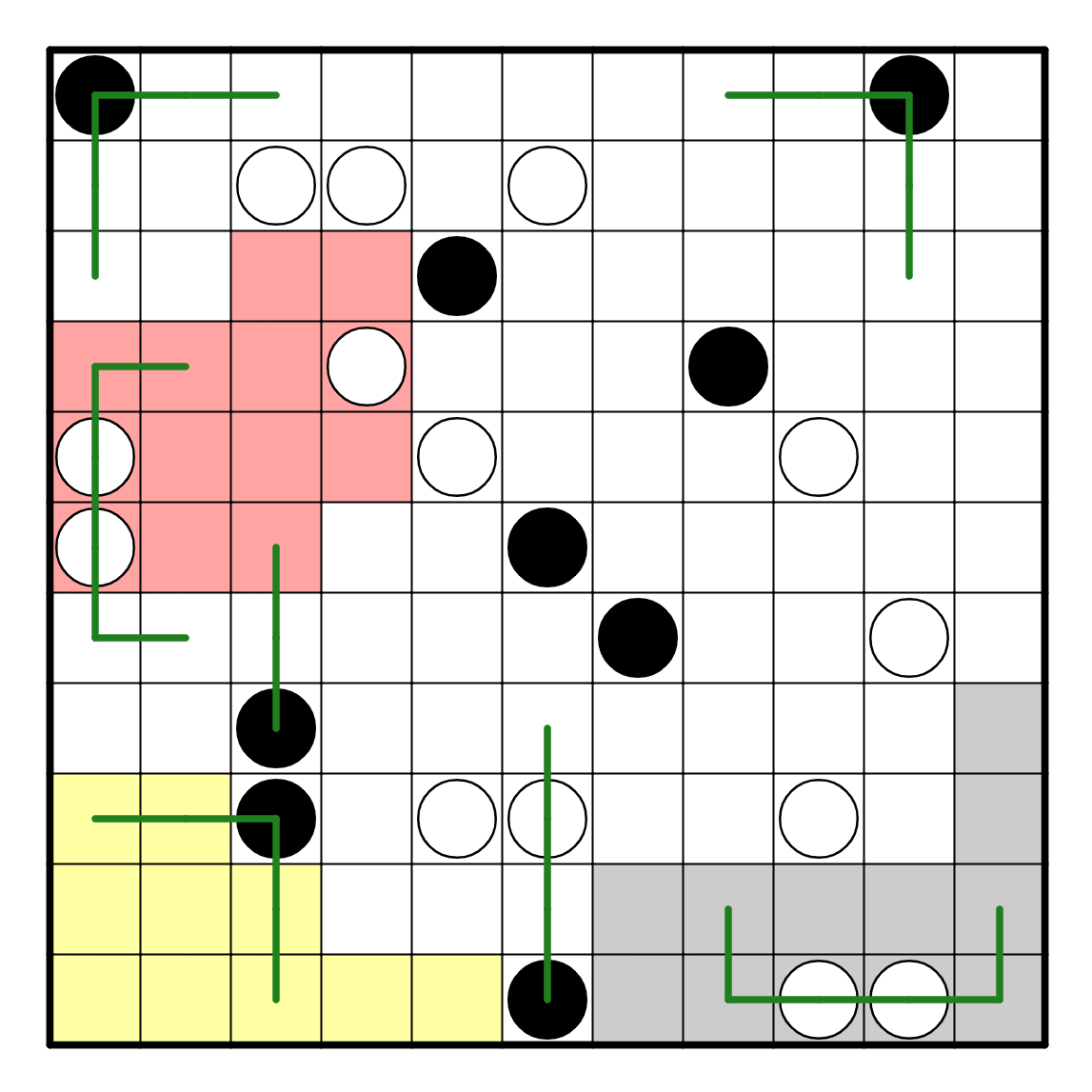
R9C5 must go up and down because of the adjacent parallel line, and
R6C6 cannot go down; if it did then the white pearl on R9C6 doesn't have
an adjacent turn. However, the key observation to make at this point
concerns R3C5. Basically, a white pearl can never be at a corner, so
this black pearl is very restricted in how it goes. If it goes up
and left, then R2C4 is at a corner and cannot be resolved; similar
issues happen with two of the other directions, meaning it must go
down and right.
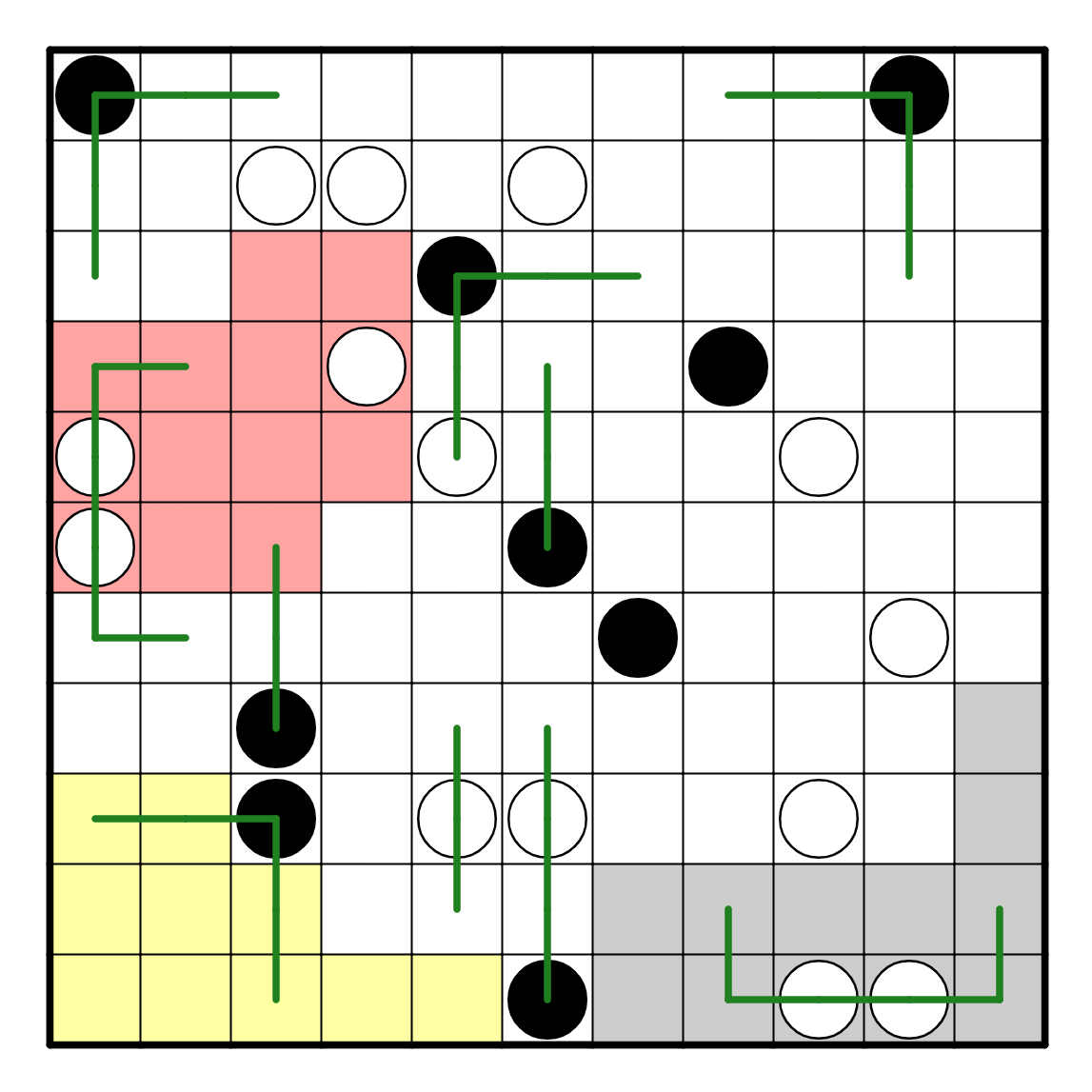
We apply a few more direct deductions from here; R2C6 and R4C4
have their directions resolved by adjacent parallel lines, R5C5
goes straight, which in turn resolves R6C6 to go right. This
now forces R7C7 to go down, and now R8C6 must turn left (it needs
to turn due to the white pearl and now it can't turn right).
R11C6 must go left, because two to the right of it is a used cell.
Finally, R2C3 and R2C6 cannot be horizontal; if they did then
they would connect to R2C6 and R2C4 would not satisfy the white
pearl rule. That's a lot of deductions, but all of them follow
directly from the basic Masyu rules.
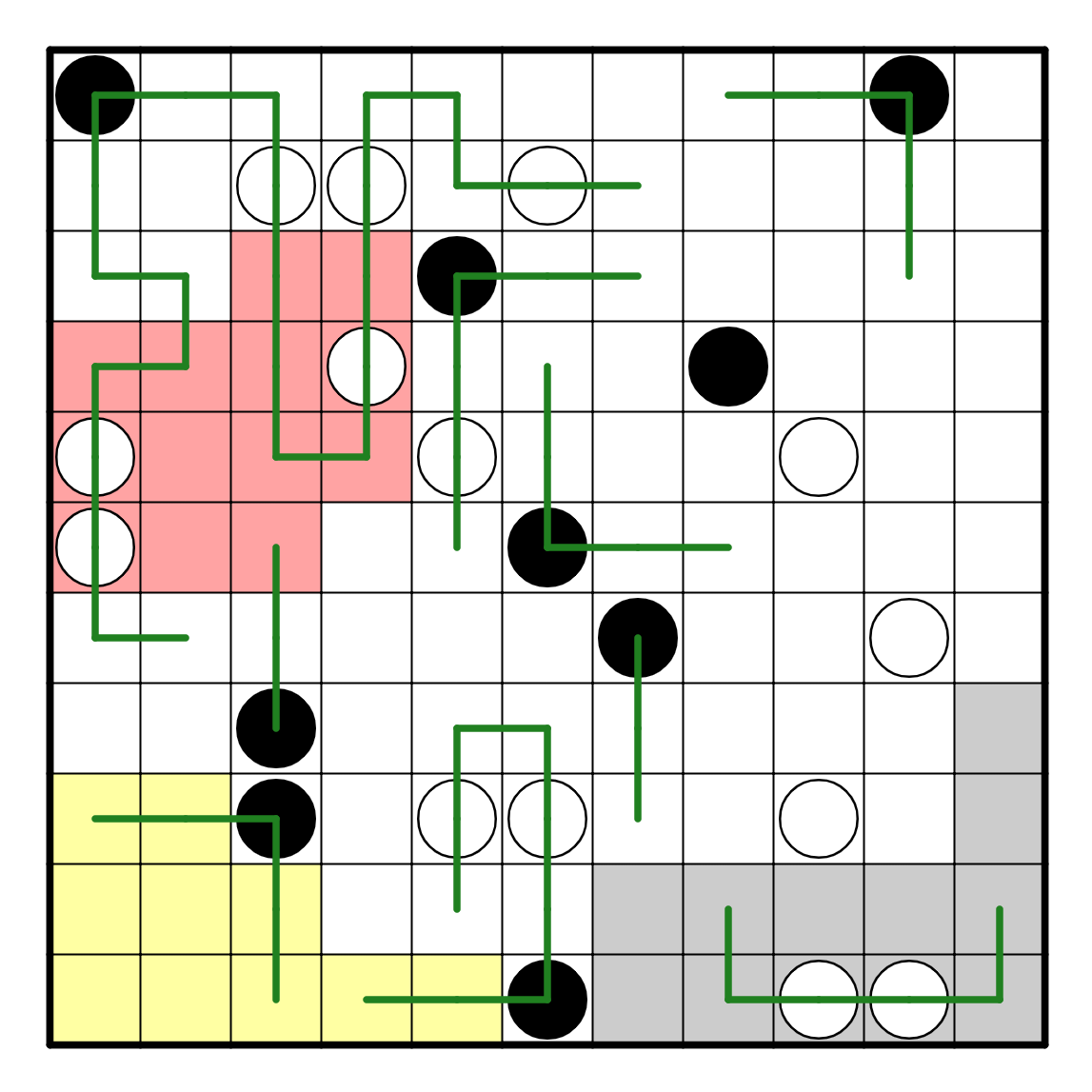
We can make some connectivity deductions now. R3C1 must go right
and then down to escape and not form a smaller loop. R5C4
goes left by the white pearl next to it, and connects to R3C3.
R1C4 goes right and connects to R2C5. R11C4 must go left to
avoid a self-loop, which resolves a bit of R10C5's path. In
fact, applying the black pearl at R8C3 and continuing similar
deductions, along with the white pearl at R5C5 causing R6C5 to turn left,
resolves the entire left hand of the puzzle.
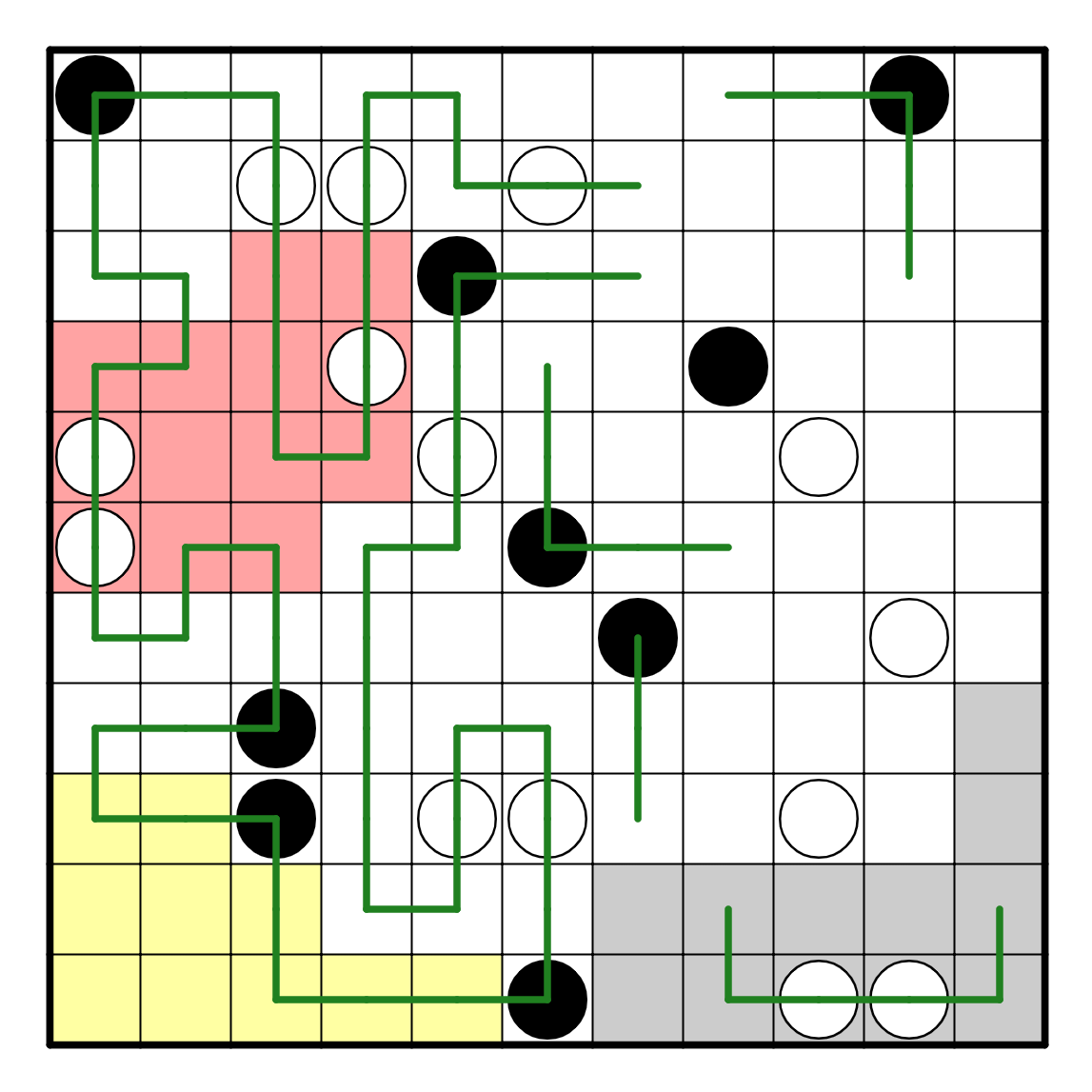
Now, R7C7 must go right because if it goes left then it cannot escape,
but the key observation right now involves R4C8. If it goes down
and left, this forms a smaller loop, which is bad. If it goes
down and right, this causes an issue with the white pearl at R5C9.
This means that it simply cannot go down, so it has to go up. Now,
R3C7 has to go down, because it is connected to R3C6 by the left
hand side of the puzzle. This resolves a bit more of the puzzle
by similar direct deductions as the rest of the puzzle.
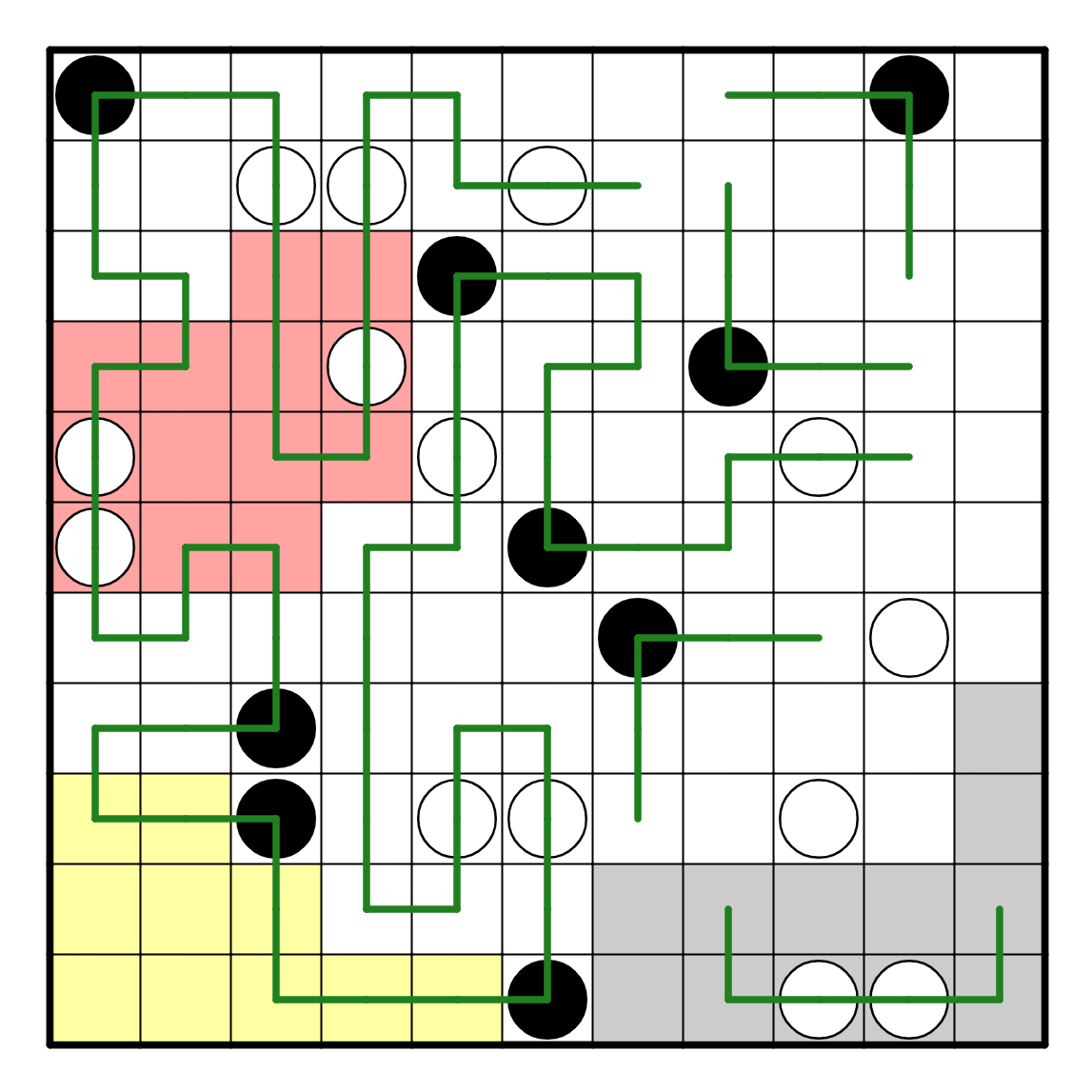
The top part of this puzzle can be resolved as well; in particular,
R2C7 must connect to R1C8, because if either of them connected to R2C8,
then the other would be trapped. This makes R2C8 connect to R3C10,
and to avoid forming multiple loops, both of these need to start going
down.
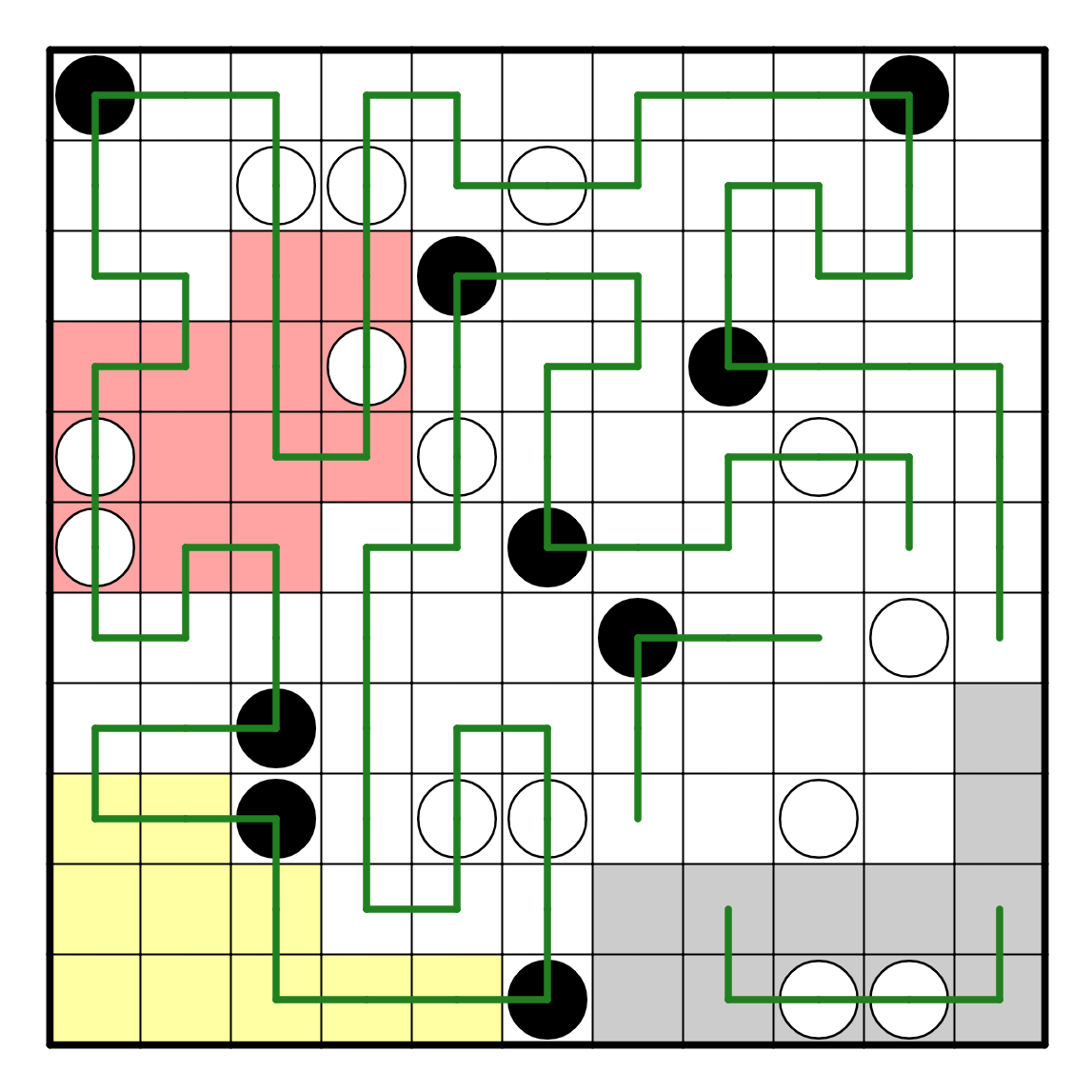
The white pearl on R7C10 must go up and down to avoid
trapping R6C10. It then turns left to connect up to R7C9. From here,
there is only one way to resolve the white pearl on R9C9. To finish
off the puzzle, just observe that R10C8 must go right to have any
hope of not trapping everything, and the puzzle resolves.
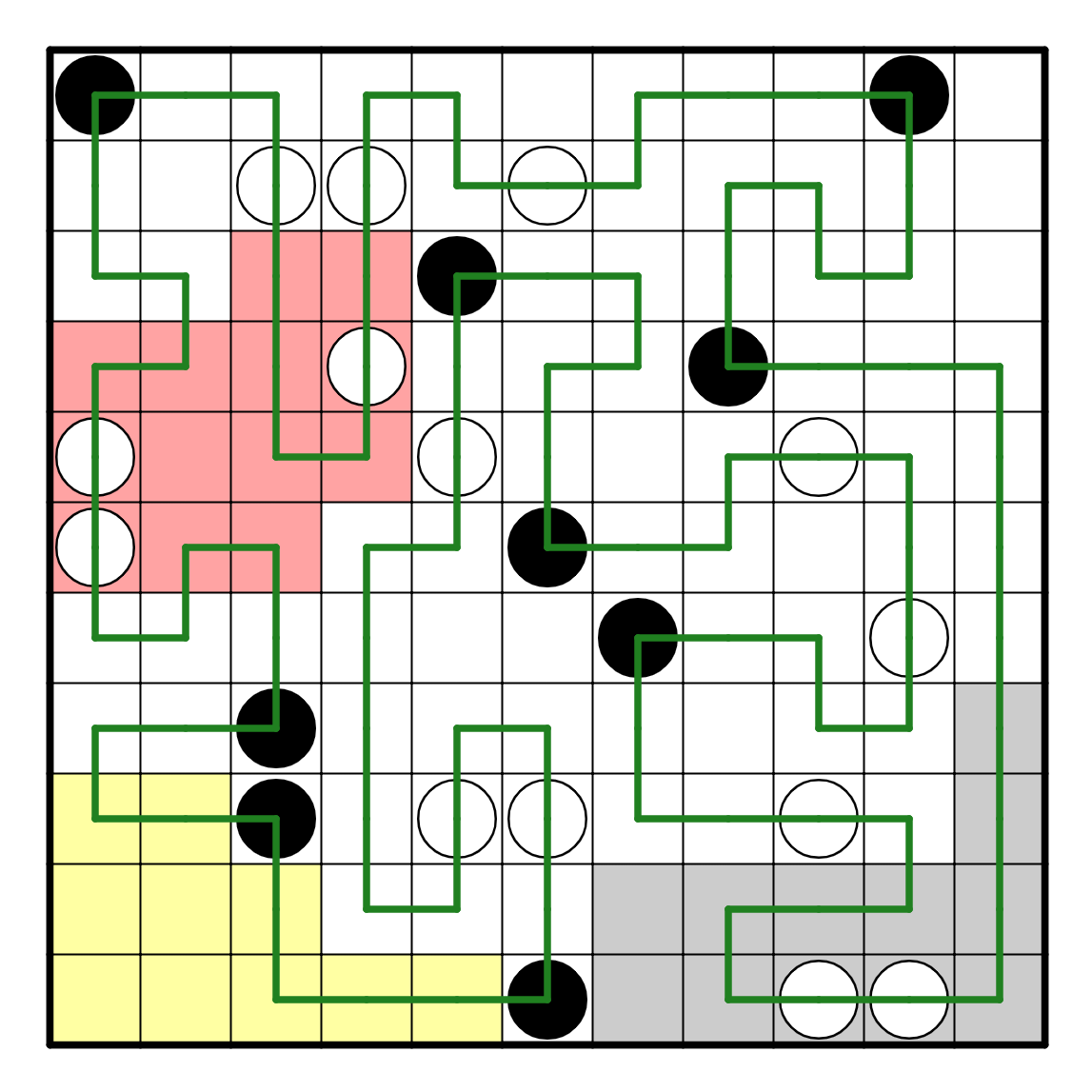
Nurikabe
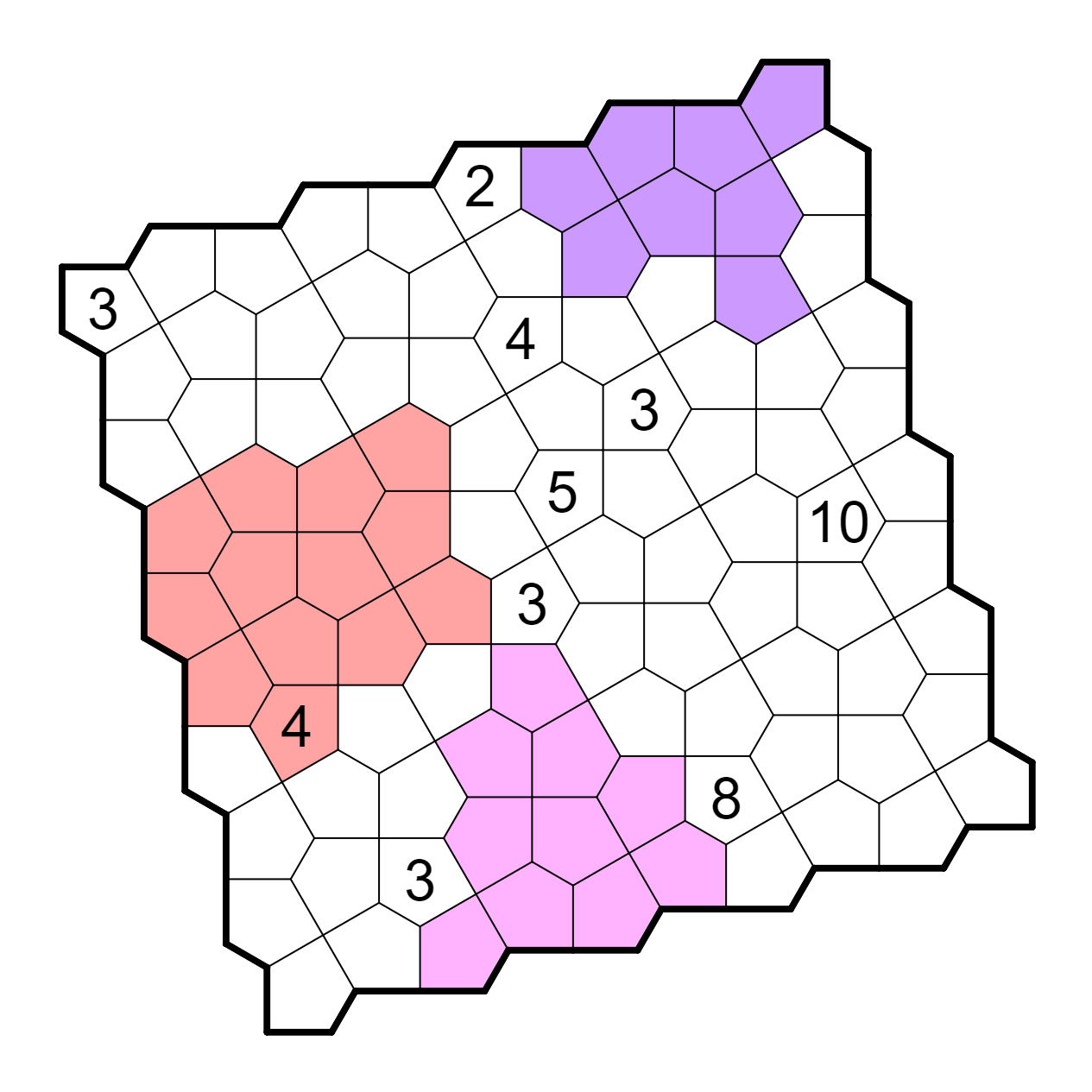
This absolutely cursed creation is actually a lot easier than it seems
at first glance. There are several cells that must be immediately
shaded to not connect two different clues together.
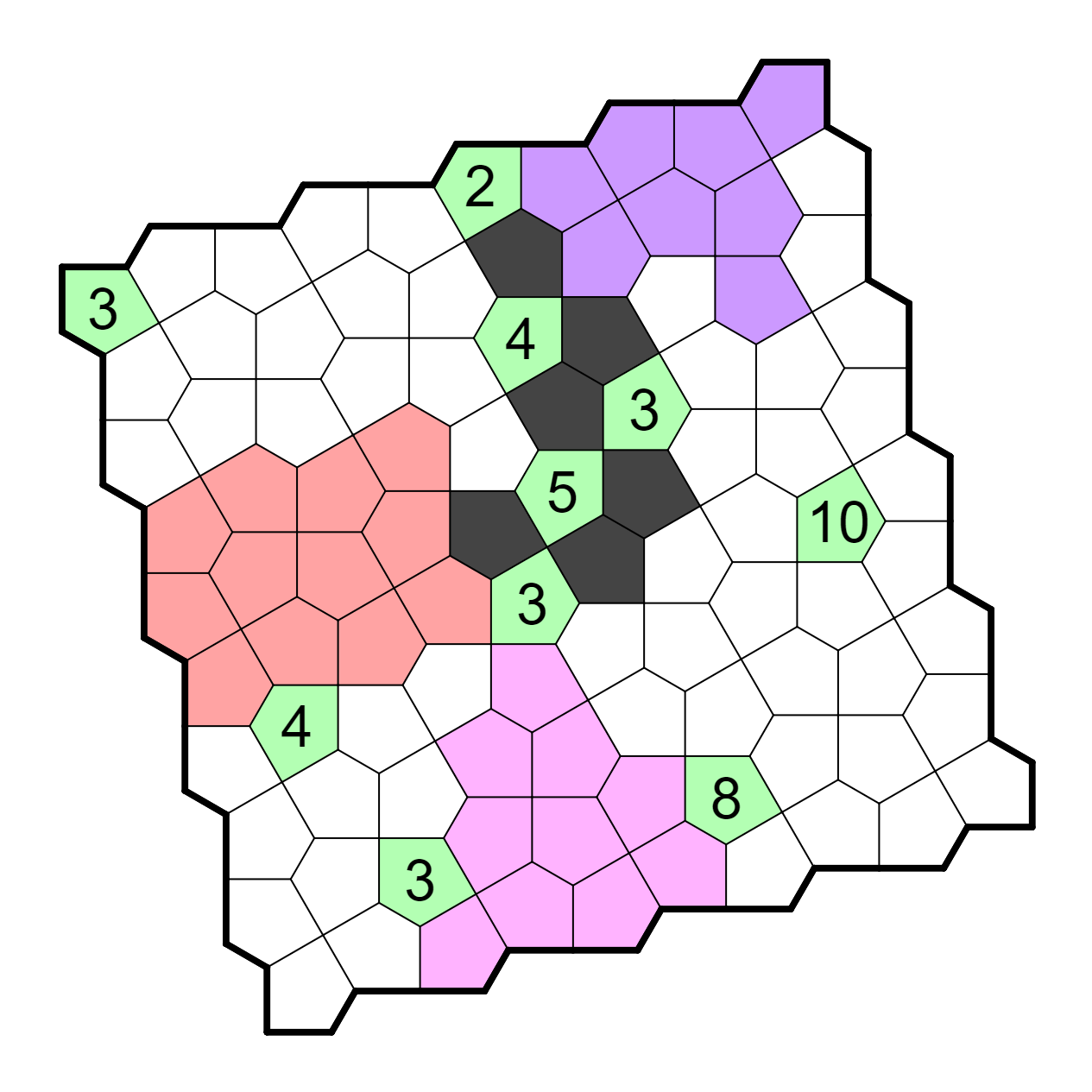
Now, the central 5 only has one way to escape, which then shades another
cell to avoid touching the 4. This 4 in turn only has one way to escape,
which shades yet another cell in relation with the upper 2. This 2
is resolved now, and both the 4 and the 5 can be shaded a bit more; in
fact, using shaded cell connectivity with the shaded cell to the
left of the 2, the 4 can be resolved entirely.
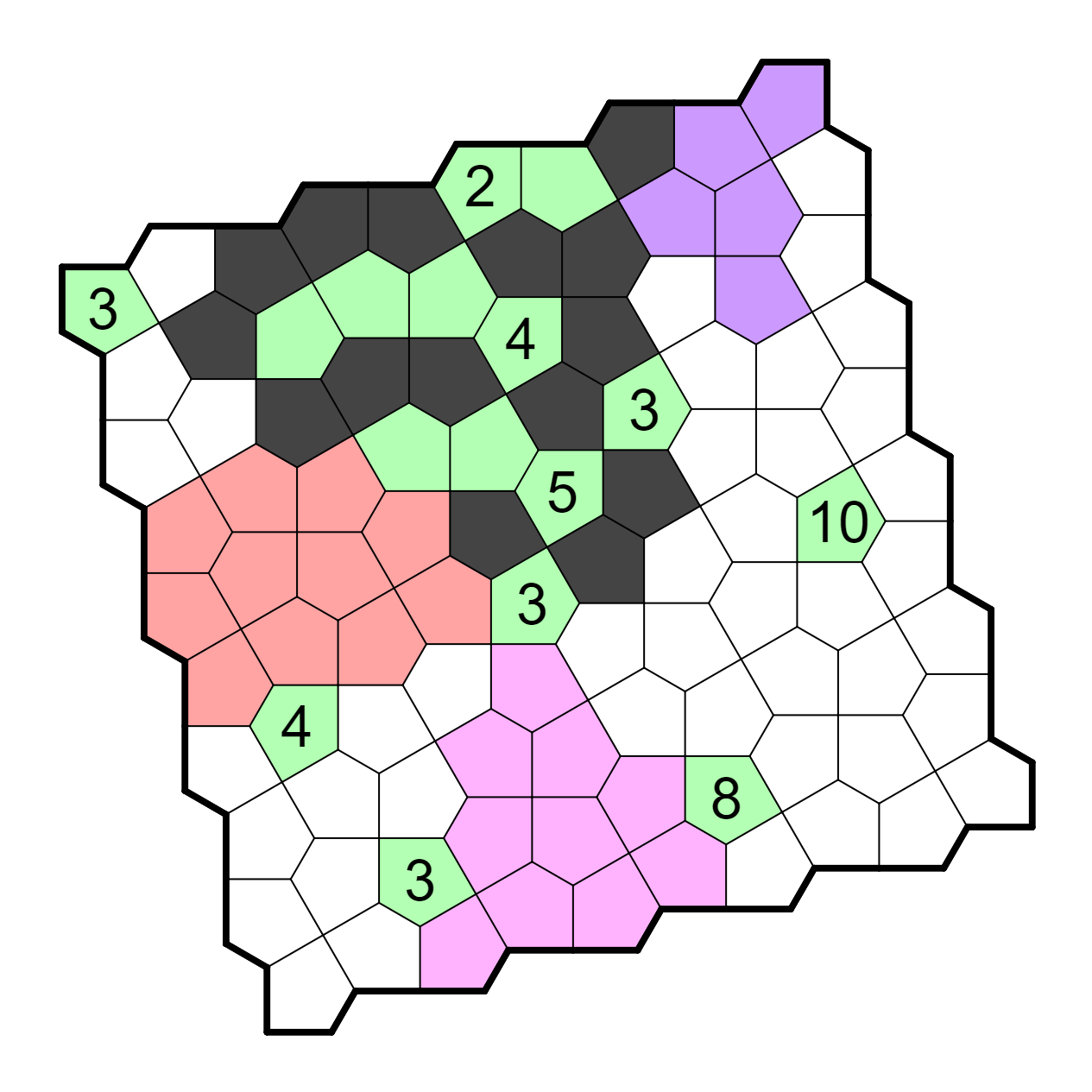
Now, we can apply the "no internal point" rule (this topology's
equivalent of the no 2x2 rule) to resolve the top-left 3. Furthermore,
two other cells must be unshaded by this rule, one above the rightmost 3
and one a bit below it. That 3 must connect to the upper unshaded cell,
since there's no other way to resolve it that doesn't touch the 10.
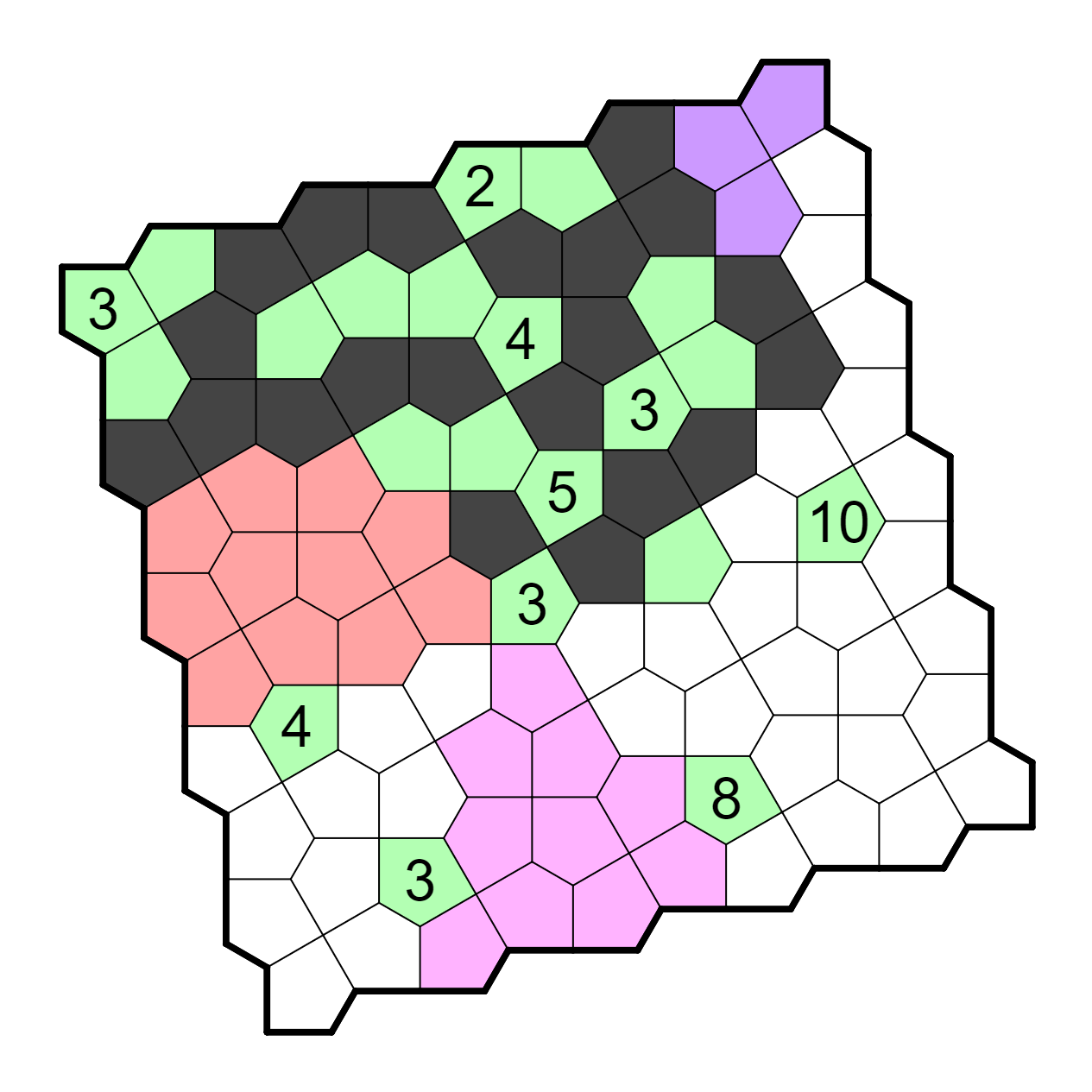
The 10 can now actually be fully resolved; the left unresolved cell on
the top row (R1C9 if you squint) must be unshaded, forcing a corridor
of unshaded cells on the right column, and in order for the shaded cells to
escape they go left afterwards, which unshades another cell by the
internal point rule, making a region of exactly size 10.
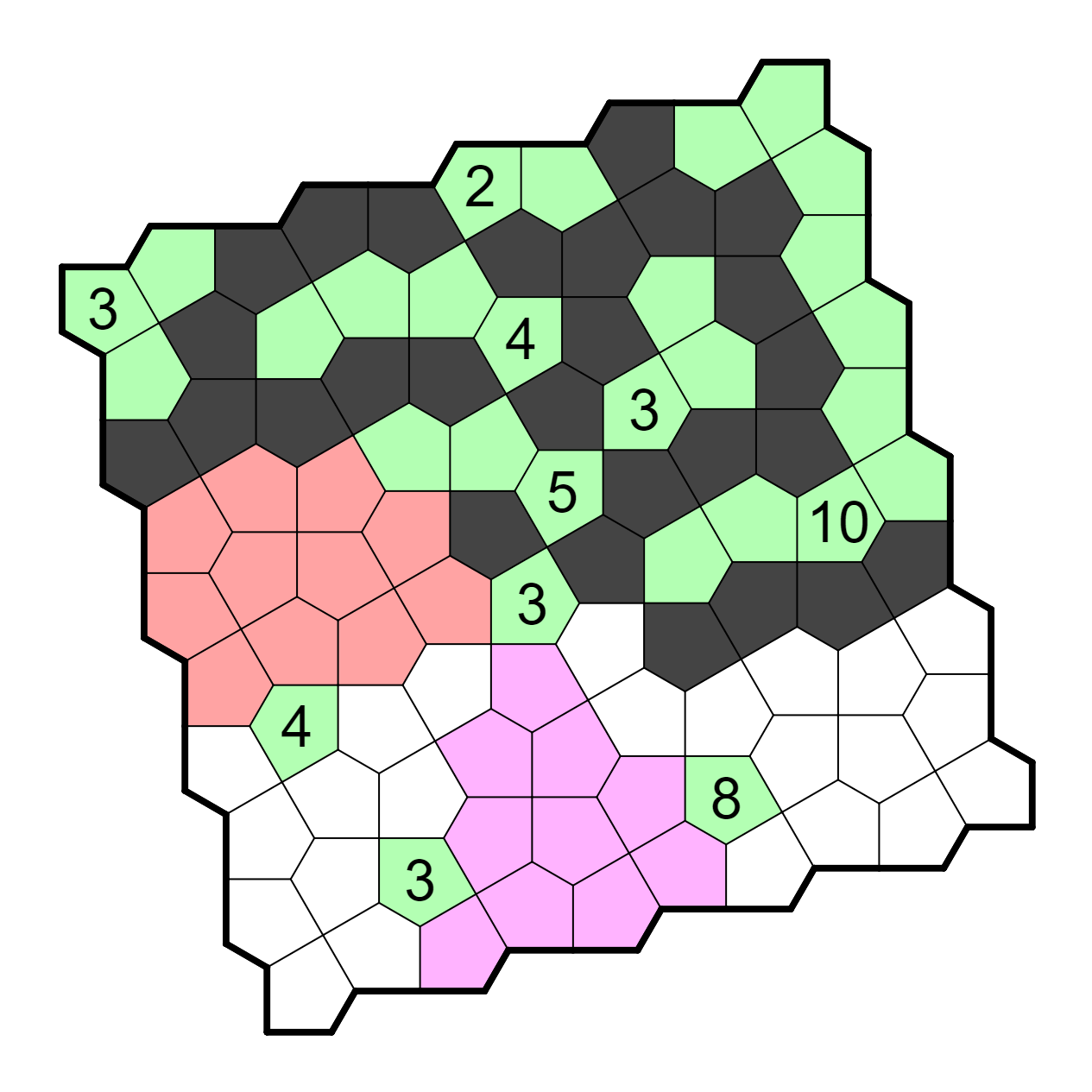
The next step involves resolving the 5-clue. There is an unshaded cell
near it by the internal point rule (R4C2) so this the 5, from R4C4,
either goes left twice or down and then left, to avoid the 3. However,
in the latter scenario, that unshaded cell connects to the 4, but it can
only do that in a region of size at least 5, which is a contradiction.
This resolves the section. Afterwards, the 4 is immediately resolved by
applying the internal point rule.
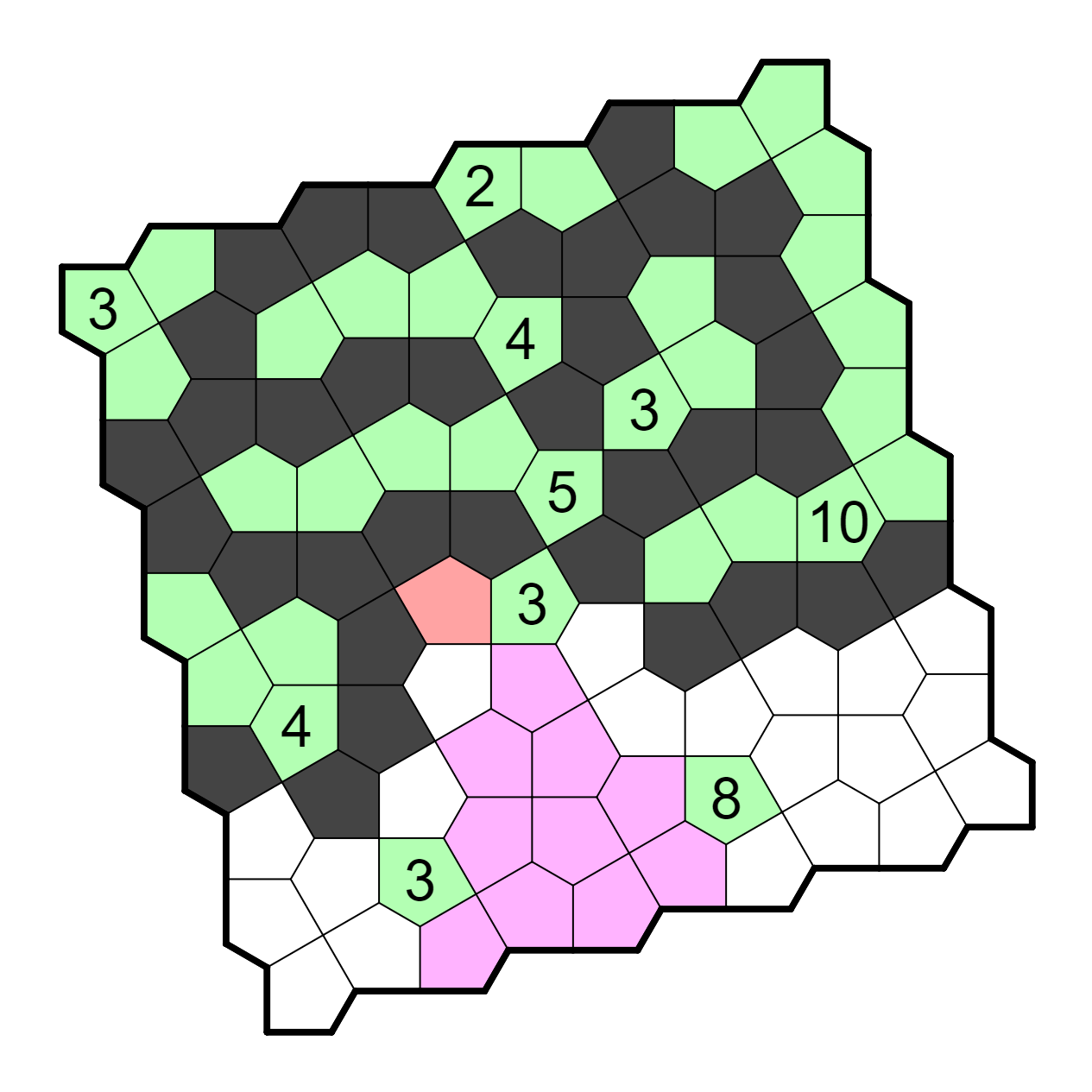
The central 3 is resolved immediately from this image. In addition, the
other 3 is quickly resolved; connectivity forces R8C1 to be shaded
and R9C2 to be unshaded. This leaves only one unshaded region left,
although the internal point rule gives us a few unshaded cells in it.
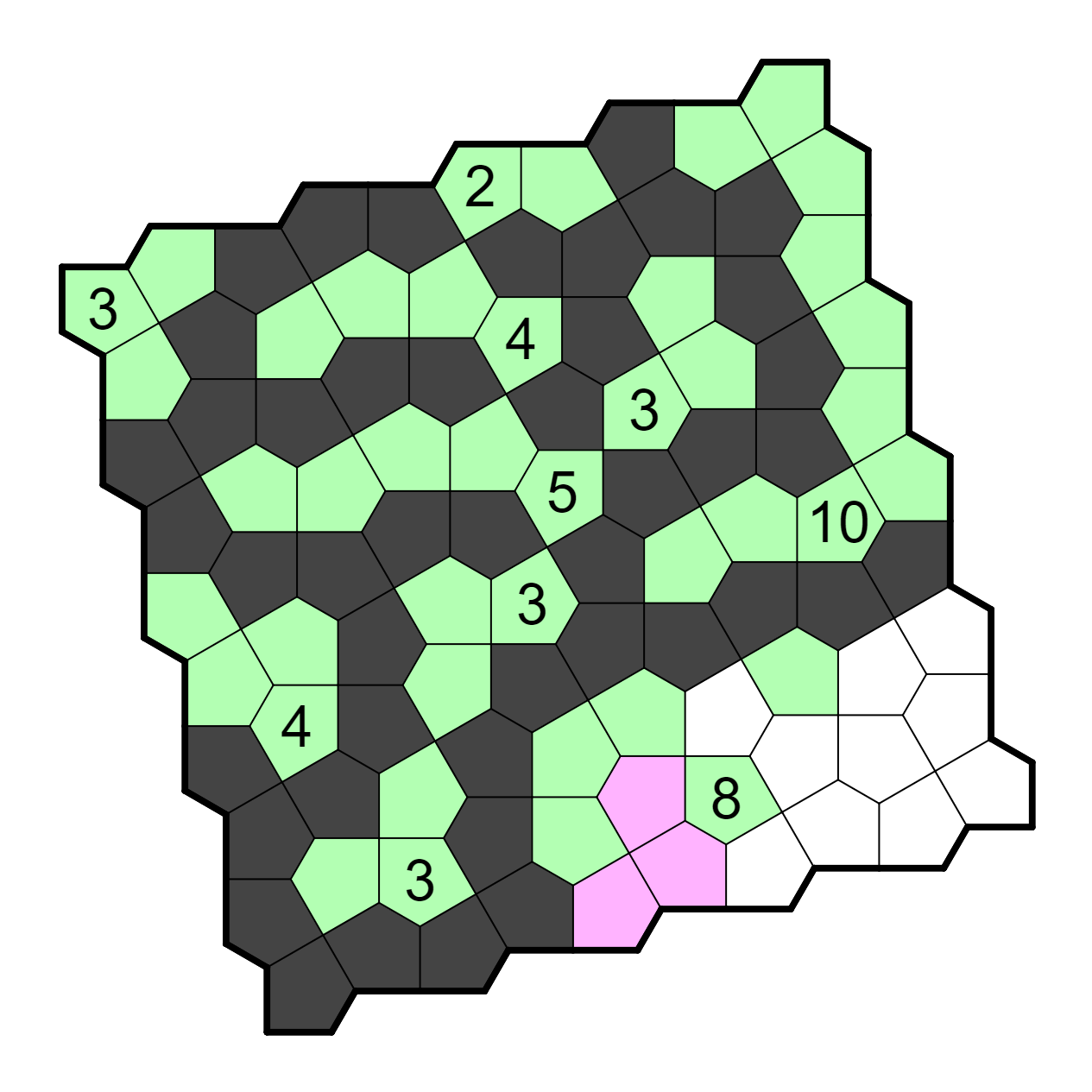
This 8 clue is very sparse; most attempts to resolve it end up forming
a shaded internal point somewhere. One logical way to resolve it is as
follows: First, among the two rightmost cells on the top row, at least
one must be unshaded to not break the 2x2 rule. Then, among the bottom
four, at least one must be unshaded for a similar reason. Finally, there
must be at least one cell to deal with connectivity (the three left cells,
the 8 clue, and the right region must all be connected, and aren't yet).
However, this totals to eight cells including the five unshaded cells already
in the grid, which means that we cannot waste any unshaded cells. This
only leaves one way to resolve it because many ways (e.g. including the
bottom right corner cell) would waste an unshaded cell.
Simple Loop
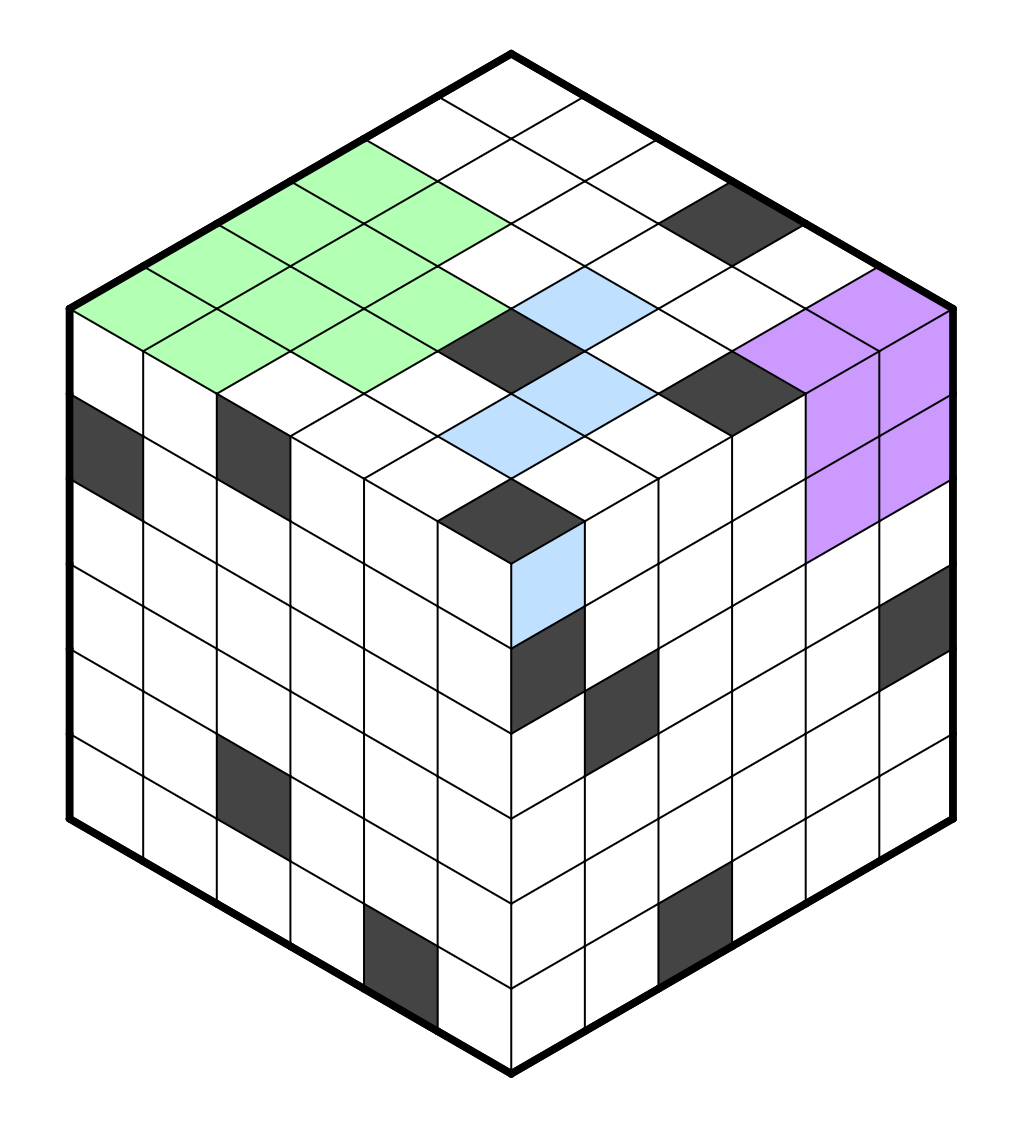
Simple Loops like this one usually flow very smoothly. The most basic deduction
in this genre is that a cell only has two adjacent cells that it can go to,
because that cell is immediately resolved.
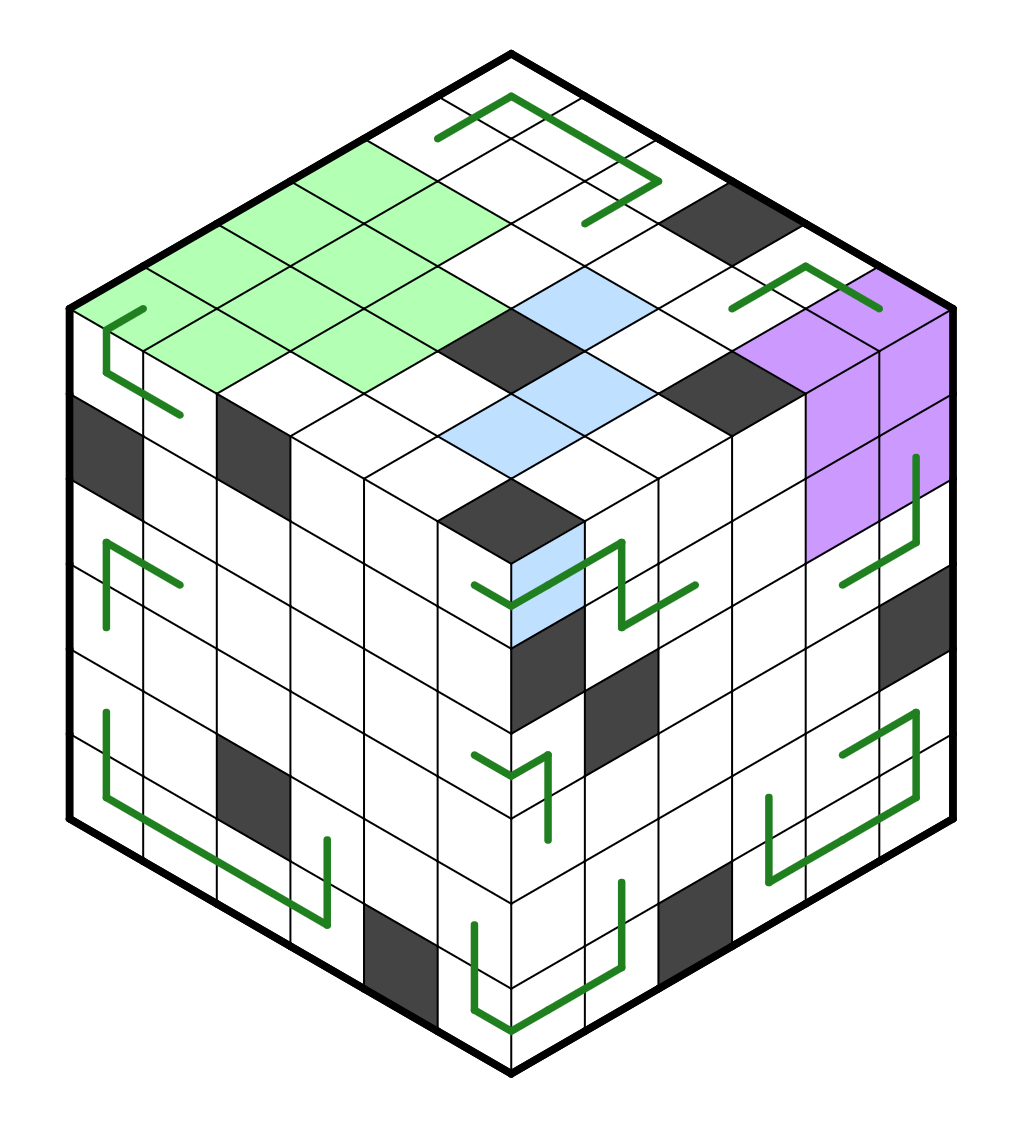
There are some more cells that can be resolved trivially (bottom left),
but the key deduction involves the right region; especially the region's
R5C1. This cell cannot go left and right, because it would form a small
loop. Therefore, it must go up. This resolves a whole bunch of information
on the right subgrid, because right's R4C2 has only two adjacent
nodes it can be connected to, and this path repeats. In fact, the entire
right subgrid resolves in a snakelike pattern.
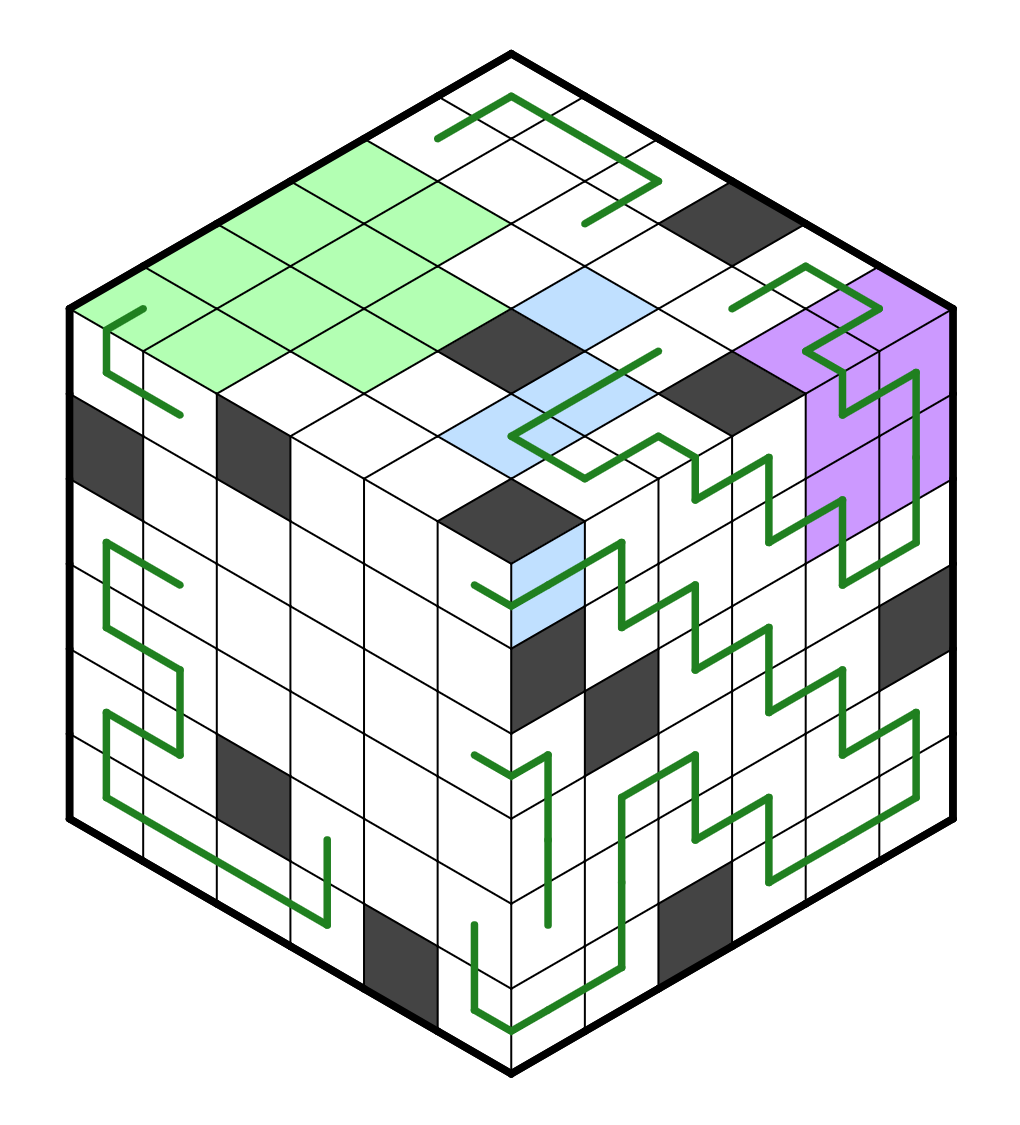
We can resolve some more based on this; on the top subgrid, we need to
not form a small loop, which forces R5C4 and R5C5 to go up. In addition,
right subgrid's R5C1 has to go left now, which resolves a lot more
in a snakelike pattern again.
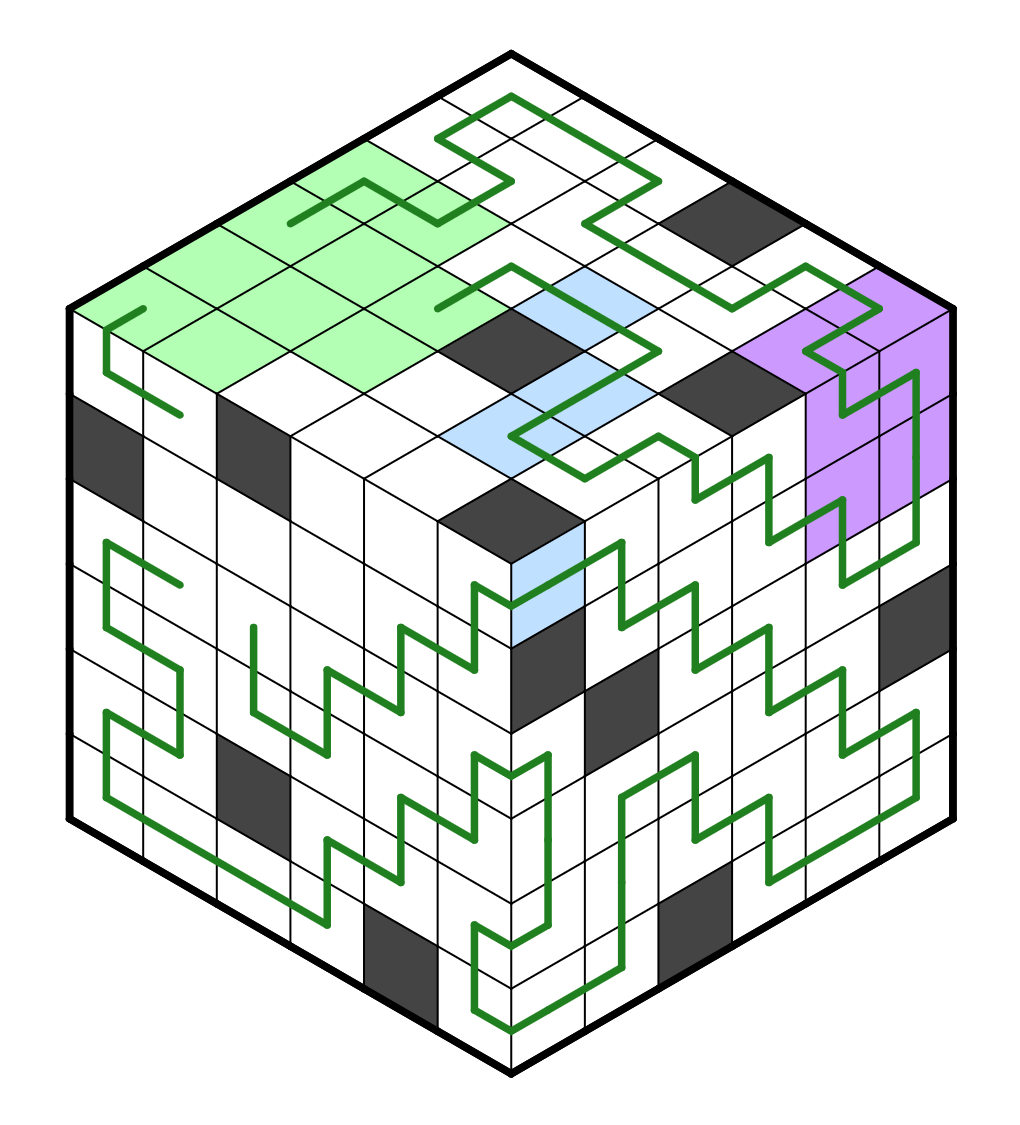
To avoid forming multiple loops, left subgrid's R3C2 and R3C3 both go up,
and the left grid is fully resolved. We can continue making basic deductions,
both two-adjacency deductions and multiple loops, to resolve the whole
puzzle.
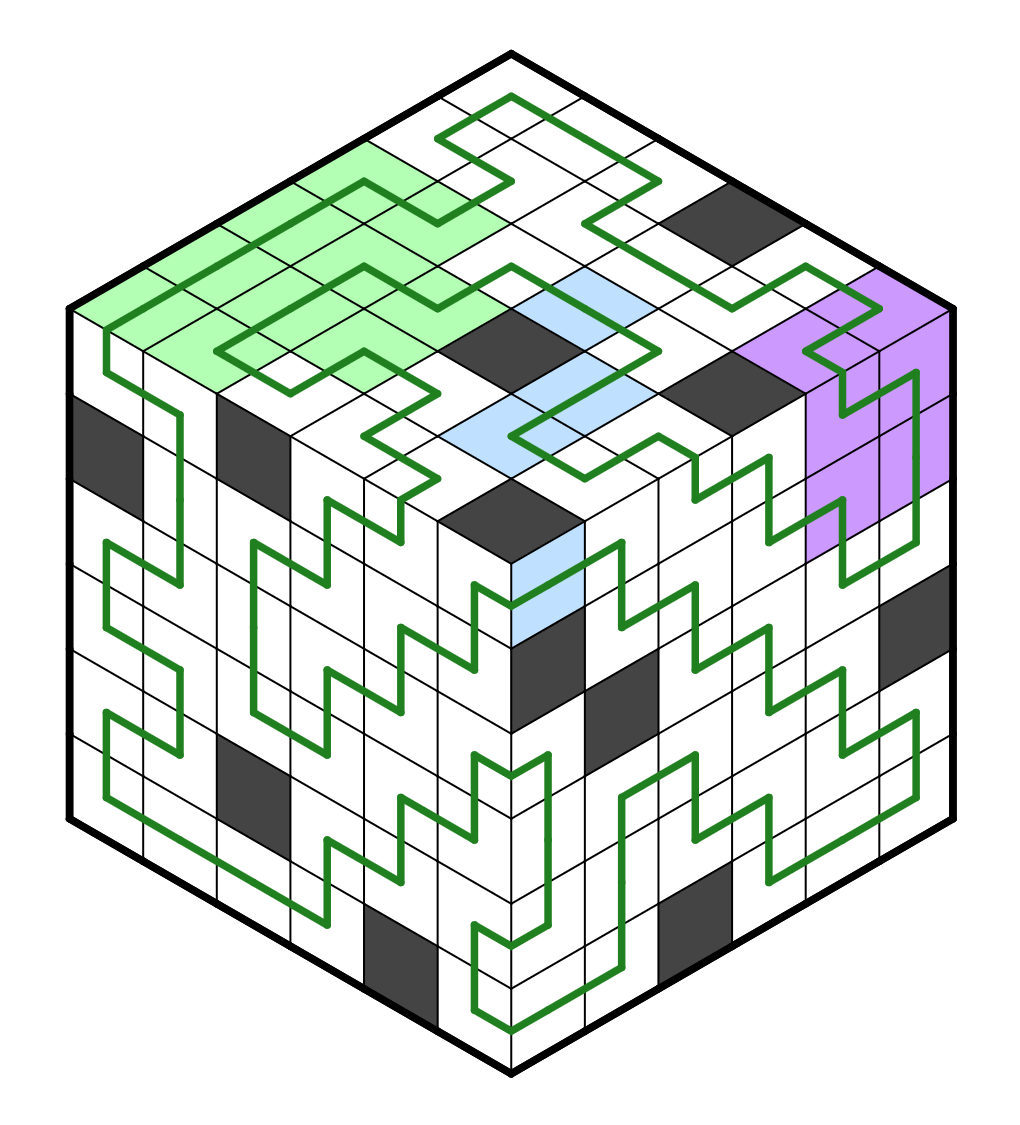
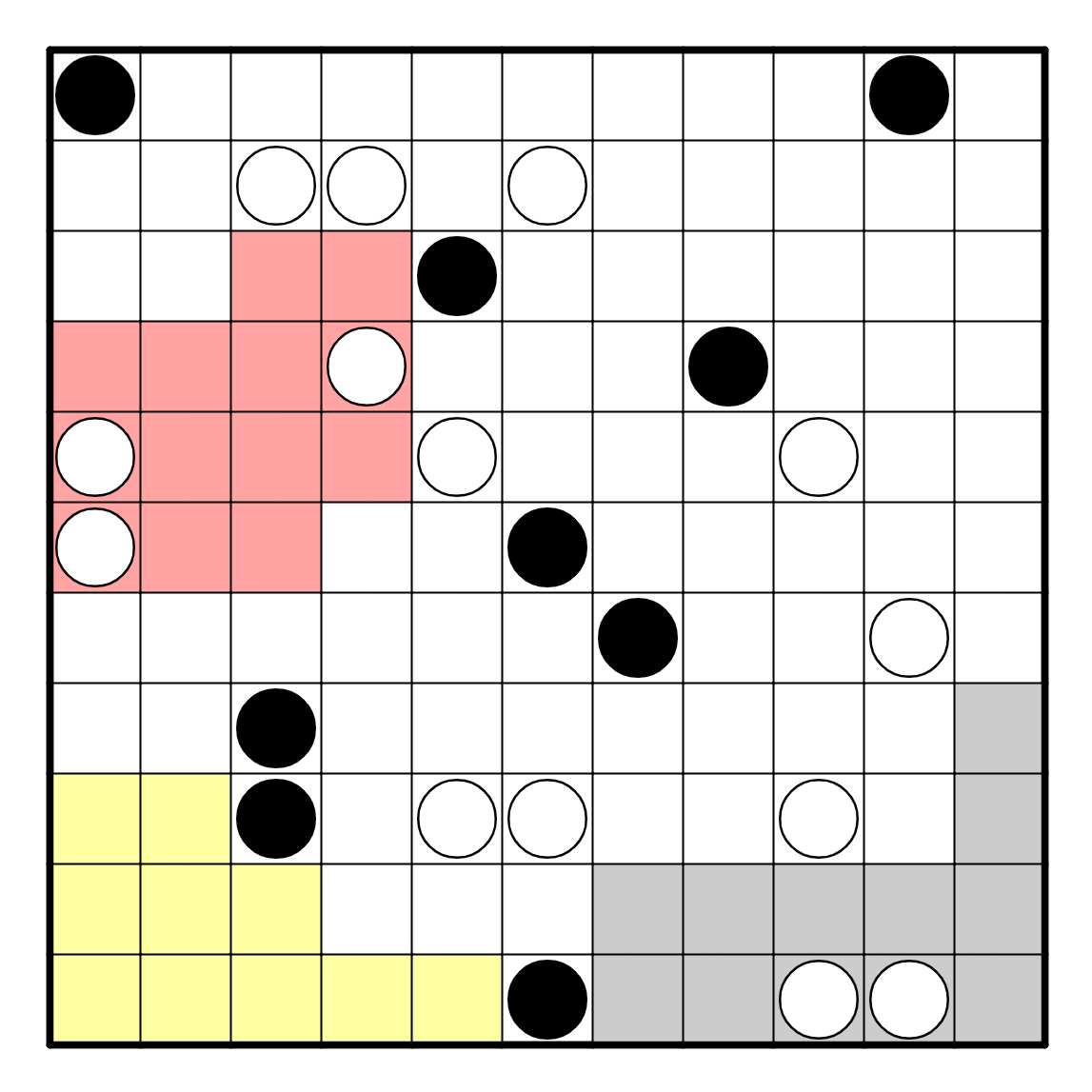
Star Battle
In this genre, a dot between some cells means there must be a star within
those cells. When there is a dot between two adjacent cells, the cells
adjacent to this pair cannot have a star.
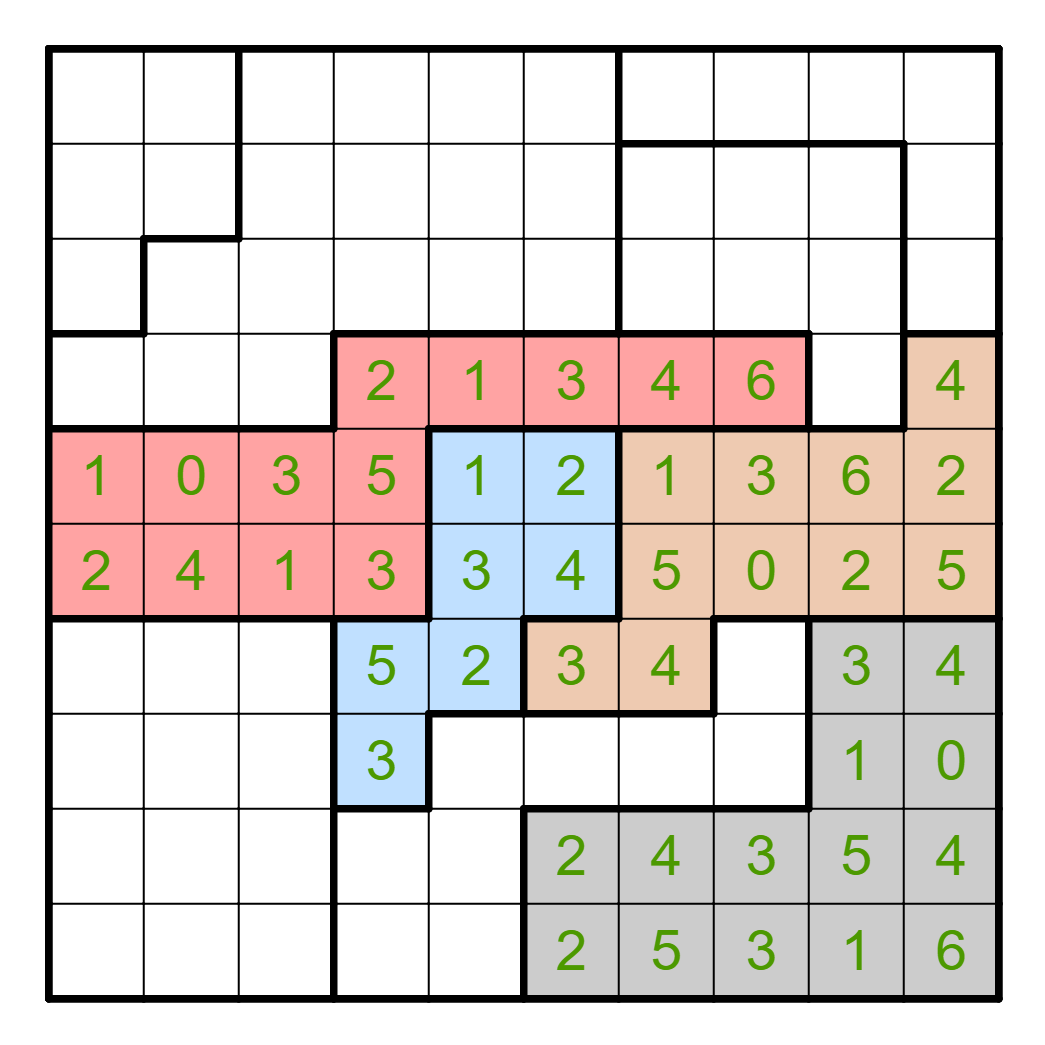
In Star Battles, you can start the puzzle by resolving smaller regions;
in particular the top left region is quite restricted. If either R2C1 or
R2C2 has a star, then no other cell in that region can contain a star.
After this, there must be a star within R1C1-2 and there must be a star
placed in R3C1.
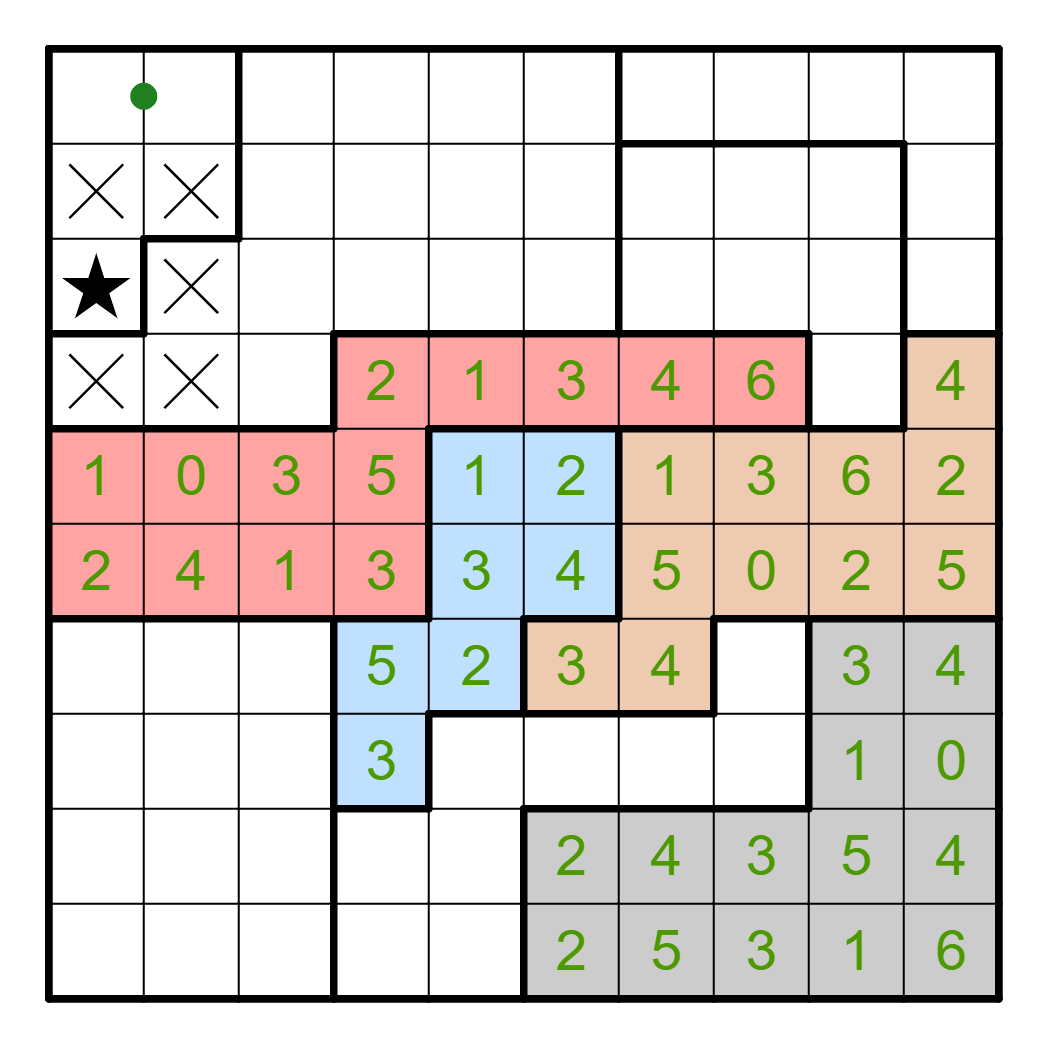
After this, we can consider what happens on the top right region. If there
are two stars within the top four cells in that region, then that makes
three stars on the top row, which is bad. So, one of the lower two cells
has a star, which blocks out R2C9 and R3C9 from having stars. Now we can
examine R4C9. If R4C9 does not contain a star, then that region now only
has a single 2x2 square where both stars need to go, which is a problem
because only one star can go in a 2x2 square. Thus, R4C9 has a star, which
resolves a star on R2C10 as well.
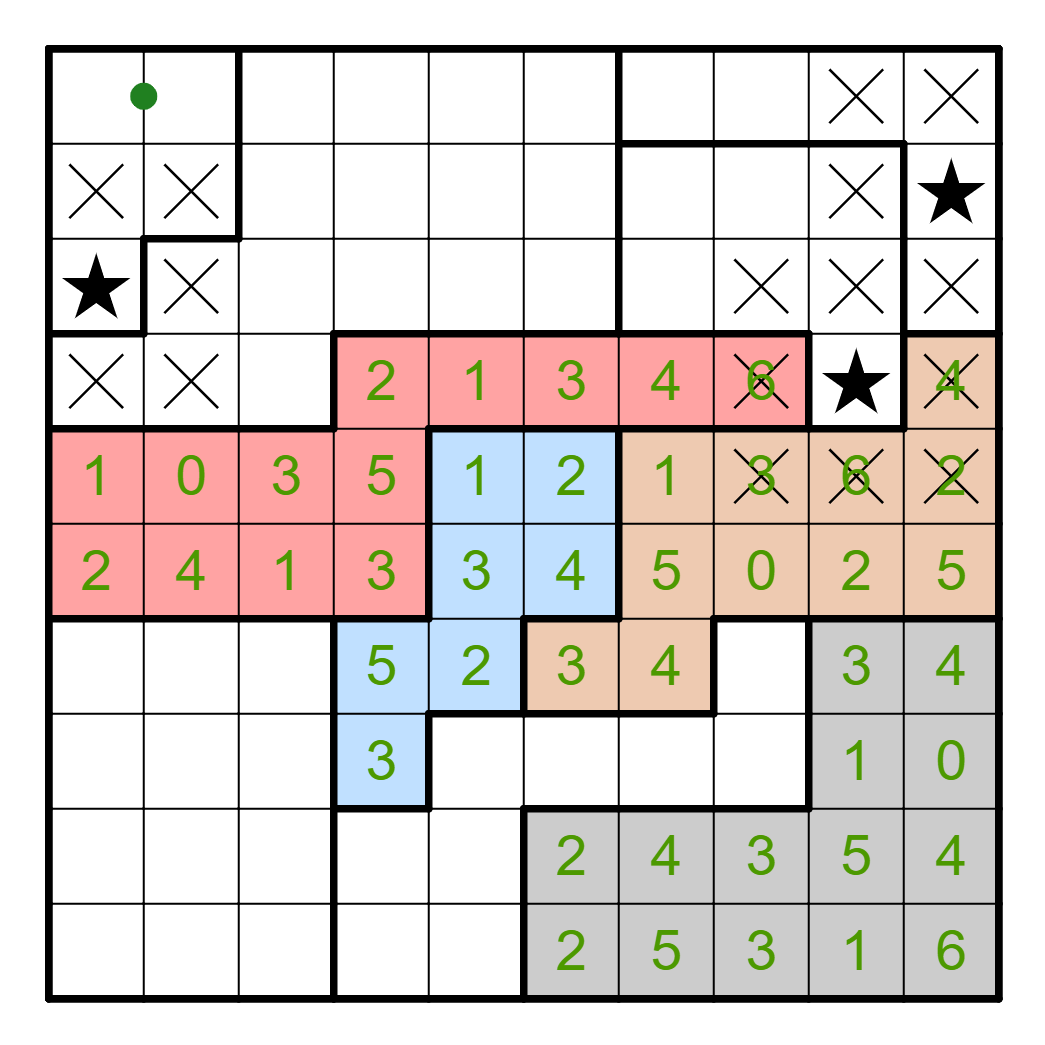
This places a star between R1C7-8, which forces a star in R3C7. Now,
we can examine the other upper region. It cannot contain a star in
Row 1, because there are already two known stars there. Similarly,
it cannot contain one in Row 3. So there must be one star in Row 2
and one star in Row 4, which means that R4C3 has a star.
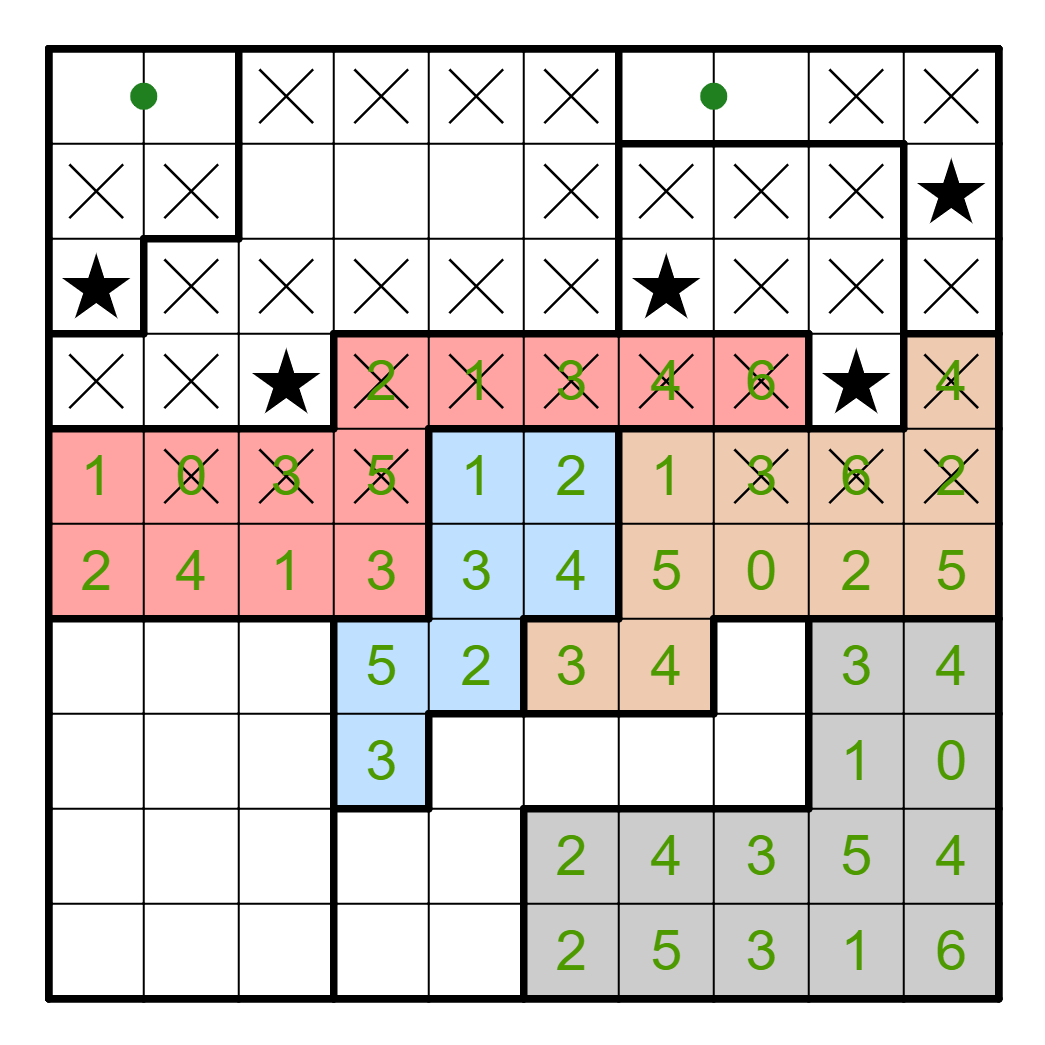
This next step is quite tricky. Consider where stars are going in Rows 5
and 6. Within the red region, two stars go in Rows 5 and 6, because
there are no other cells. Within the blue region, at least one star
goes in Rows 5 and 6 (in fact, exactly one star). Within the brown region,
at least one star goes in Rows 5 and 6. However, this makes four stars,
which is the number of stars that can go in those two rows. This means
that either R7C6 or R7C7 must contain a star in the brown region, which
means the cells above and below this pair don't have a star.
Similarly, one of the bottom three cells in the blue region contains a star,
so there cannot be a star in R8C5.
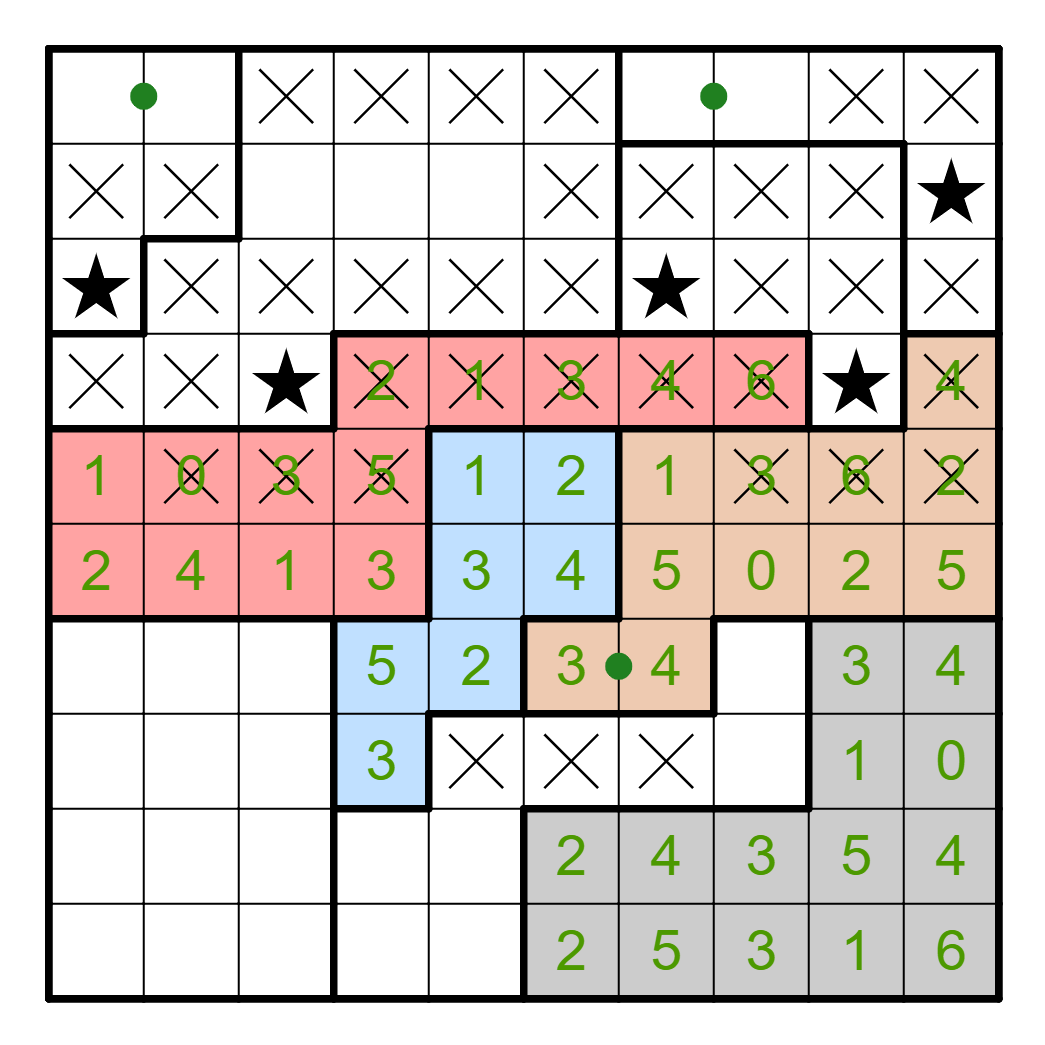
Now, consider the bottom-middle region. There must be at most one star
within R9-10C5-6, so there must also be one star in R7-8C8. This
actually resolves the pair to the left of it and means that R7C6 has a
star.
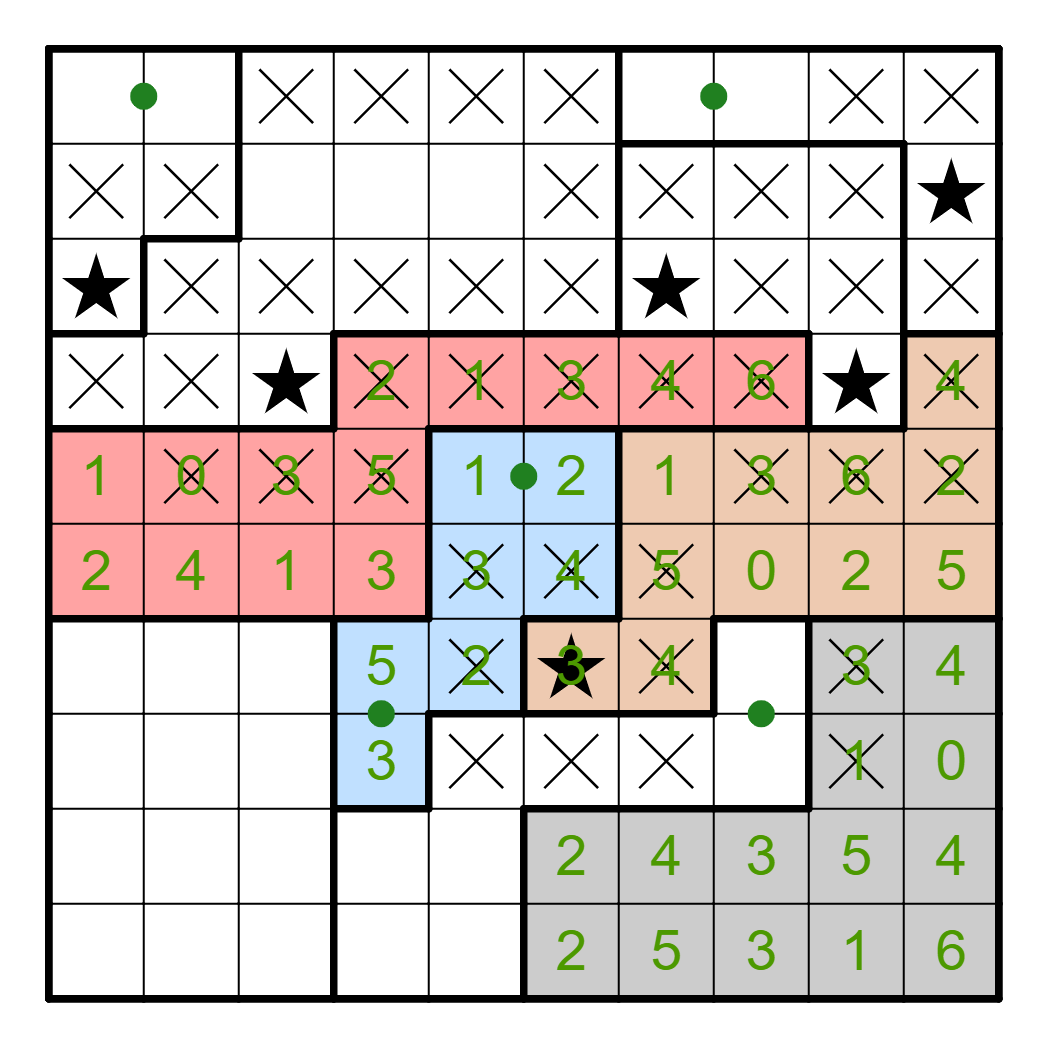
We can do more with the red region. There must be one star in the left
three (still yet to be marked as wrong) cells, and one star in the right
two. This forms a pair that resolves R7C4 as not a star, and R8C4 to have
a star. There is also now a pair in R10C4-5.
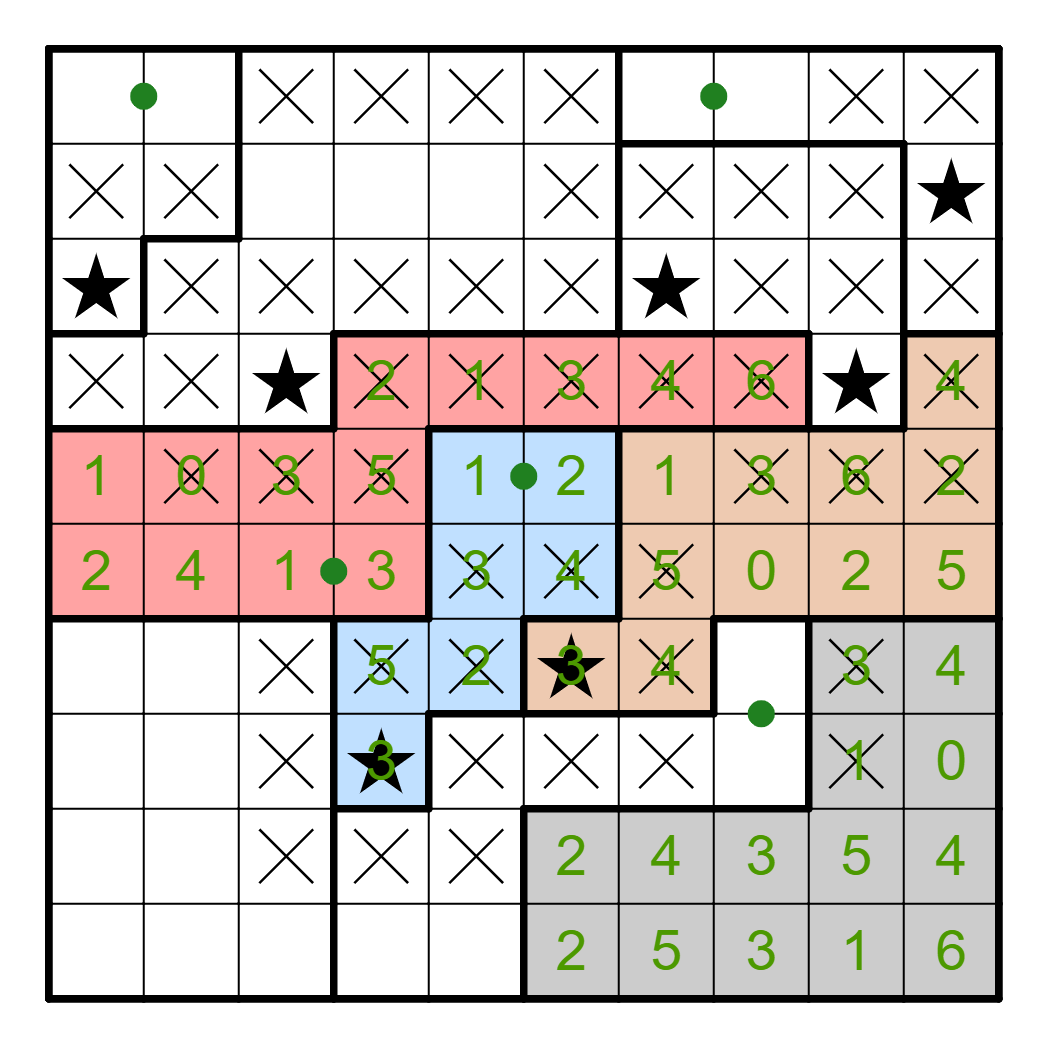
At this point we should consider the left two columns. There are two
stars contributed to it by the top left region, and the red region
must also have a star in the left two columns. So, the bottom left
region must have at most one star in these two columns, which means
that R10C3 must have a star. Because this is the second star in column 3,
this resolves a lot of information immediately; R10C5, R6C4 both contain
stars, which then places stars in R2C5 and R5C6 as well. Also, there
is a star in R5C1 since that's the only way to get two stars in Row 5,
which then places a star in R1C2.
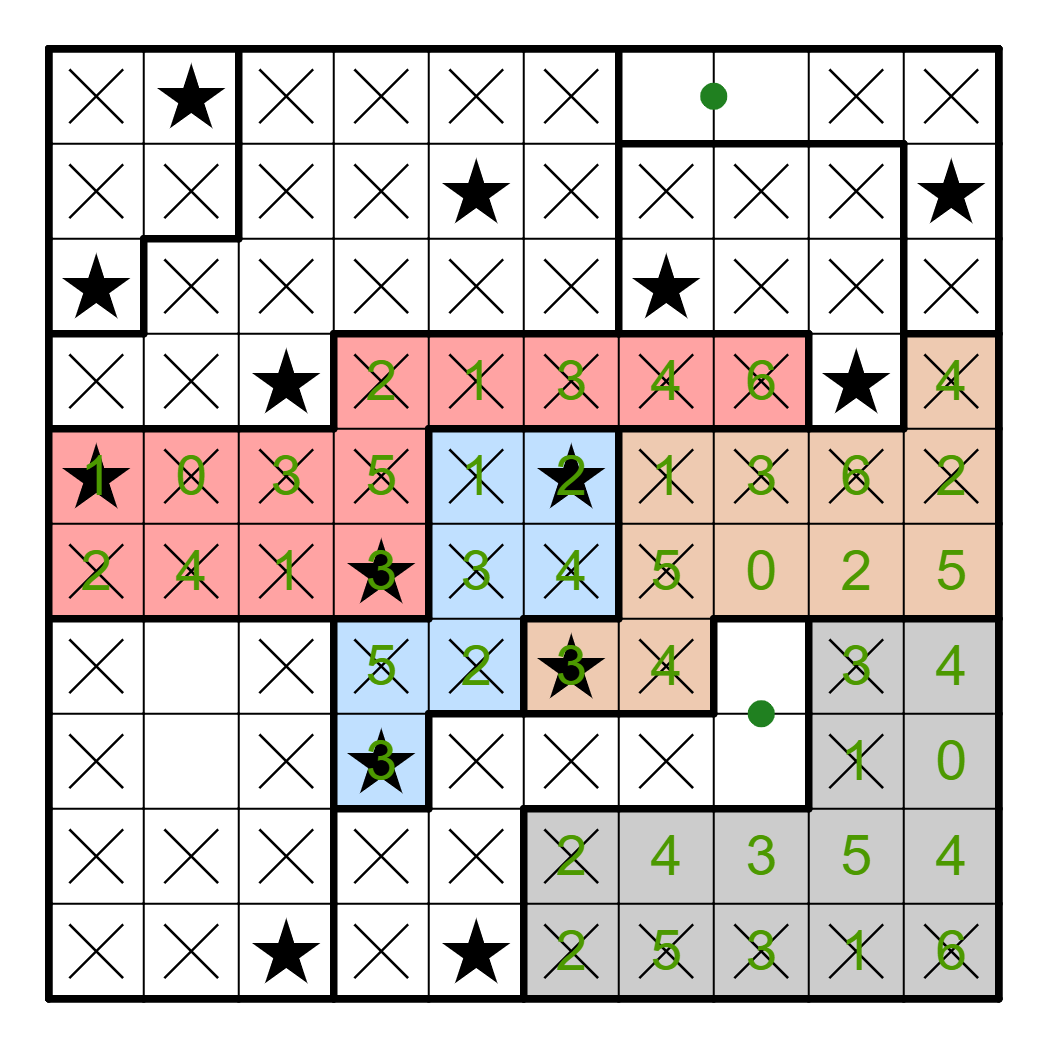
Now, let's consider row 9. Almost every cell from it does not have a star;
the only four that are still possible are all in the gray region, so
they indeed come from there. This places a pair in R9C7-8 and another in
R9C9-10. This forces a star into R7C8.
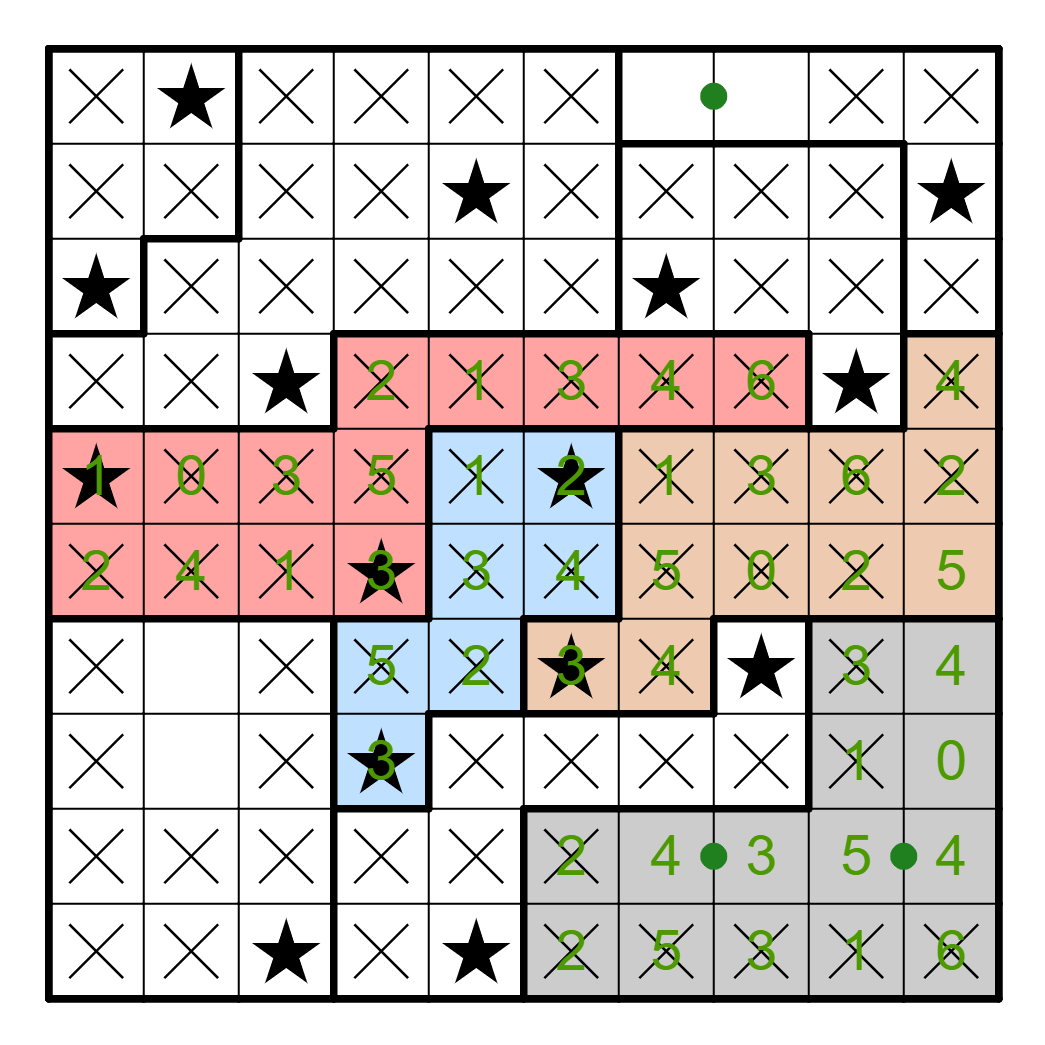
After this, the rest of the puzzle is straightforward. Only R6C10 can
contain the second star in Column 10, which resolves the gray pairs
and the pair from Row 1. Finally, R8C2 contains a star.
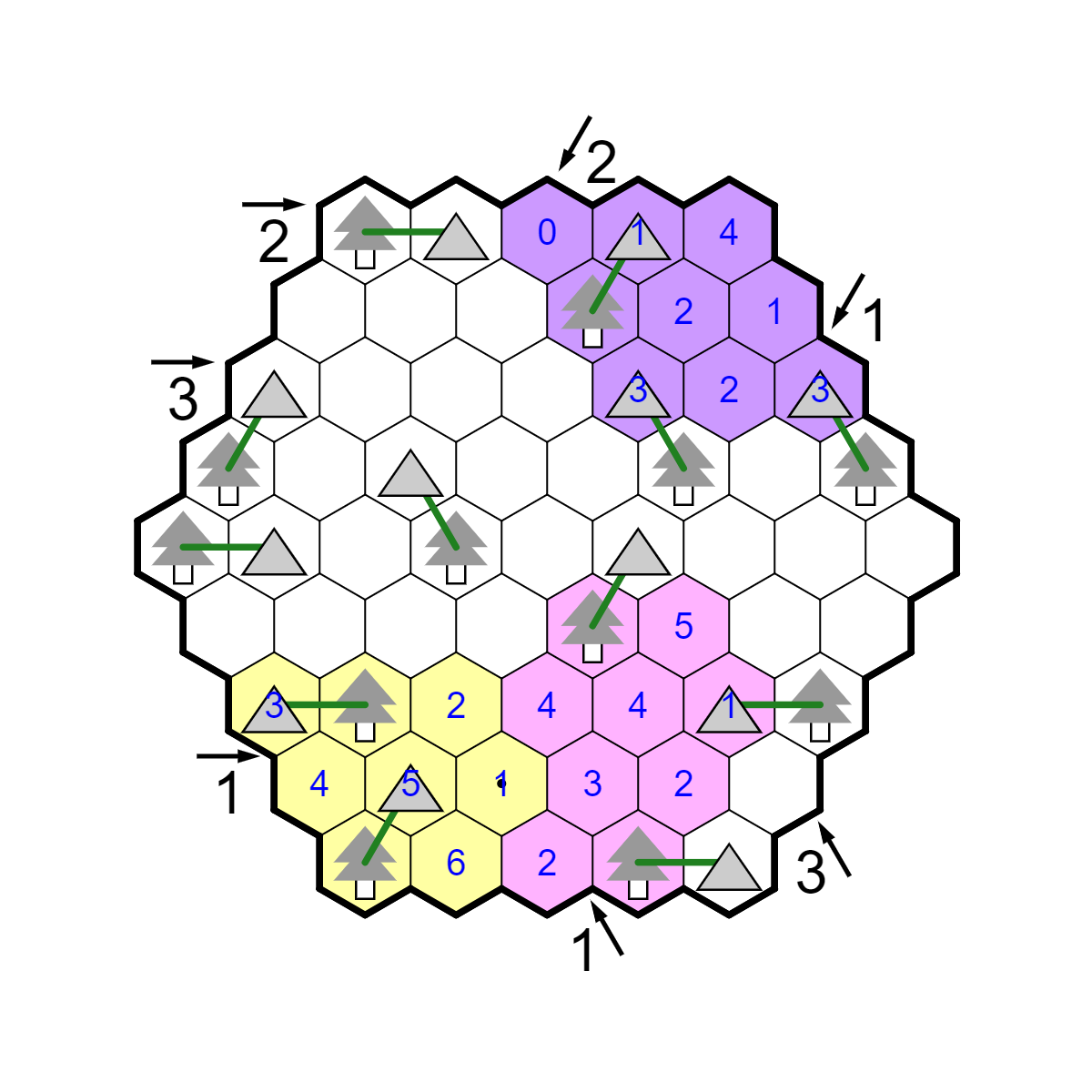
Tents
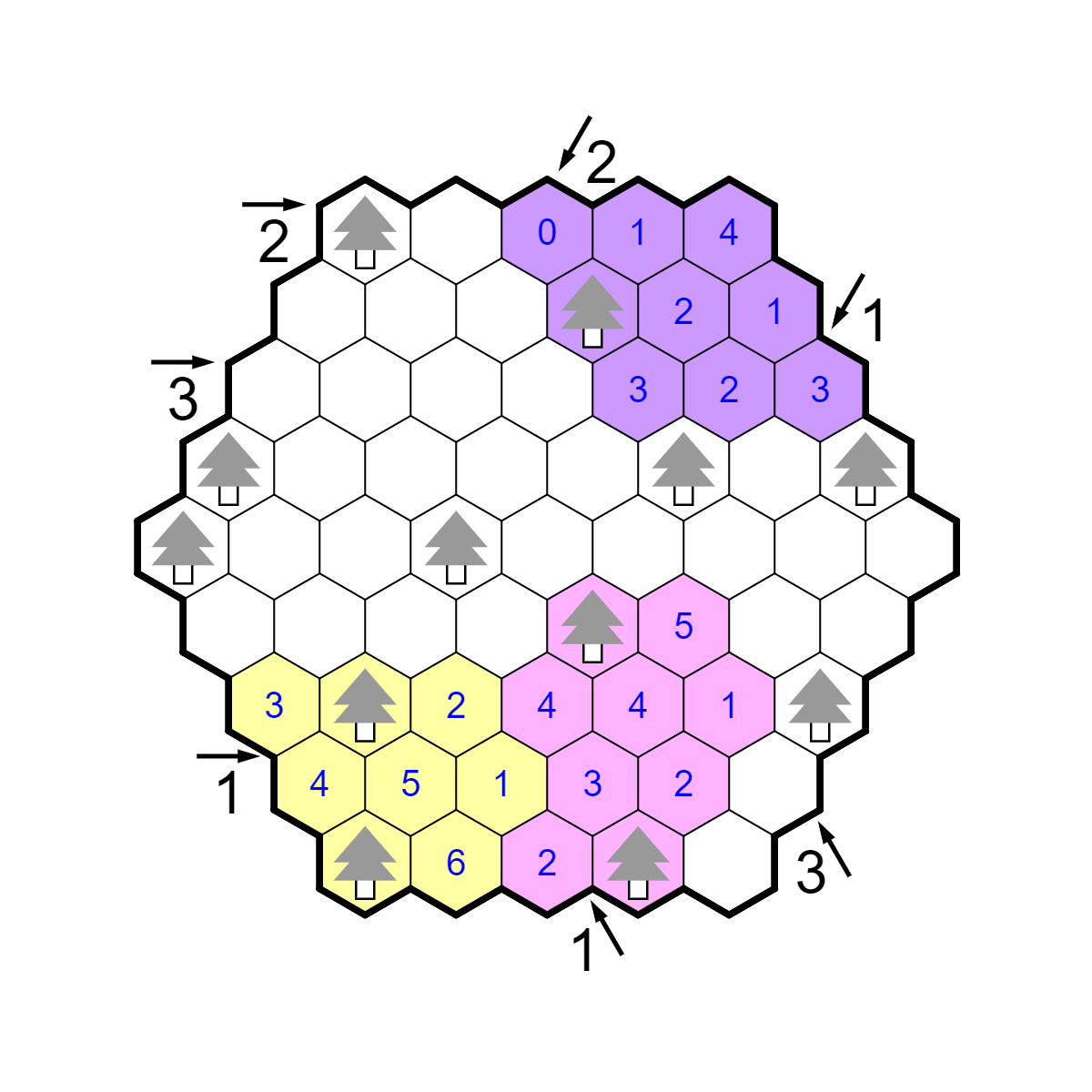
This is kind of a weird puzzle, but it's not too bad. The first observation
is that there are some cells we know cannot contain tents, because
there are no trees directly adjacent to them. Most importantly, R3C2 and
R3C3 do not contain tents, so the 3-right clue is very restricted. There
must be a tent in R3C1, since only one of R3C4-5 and only one of R3C6-7
can contain a tent. In addition, because R1C5 does not have a tent,
there is only one way to place the tents in the top row to satisfy the
2-right clue: One on R1C2 and R1C4. These three tents can be connected to
their only adjacent trees.
Now, R3C4 cannot have a tent because the tree in R2C4 is already used.
This resolves row 3 to have tents on R3C5 and C7. In addition, the 1
down-left clue is satisfied, which marks quite a few cells as not
having tents.
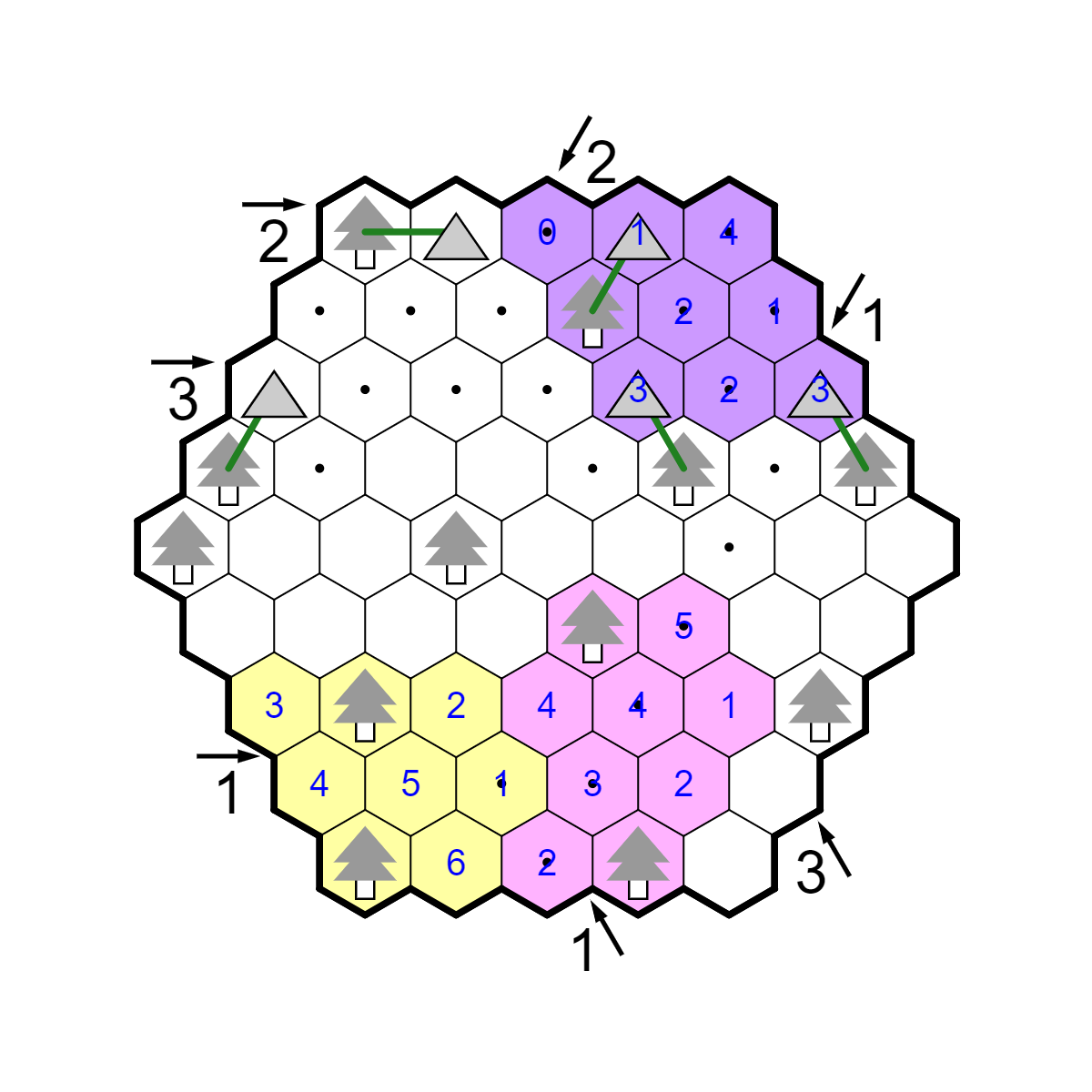
Consider the 2 down-left clue. There are four possible locations for tents
that split into two pairs: R4C3, R5C3, R6C2, R7C1. But the tree in R5C1
restricts this; its tent is either in R5C2 or R6C1, and in either case
R6C2 cannot also contain a tent. This places a tent in R7C1, which then
places one in R5C2 and R4C3.
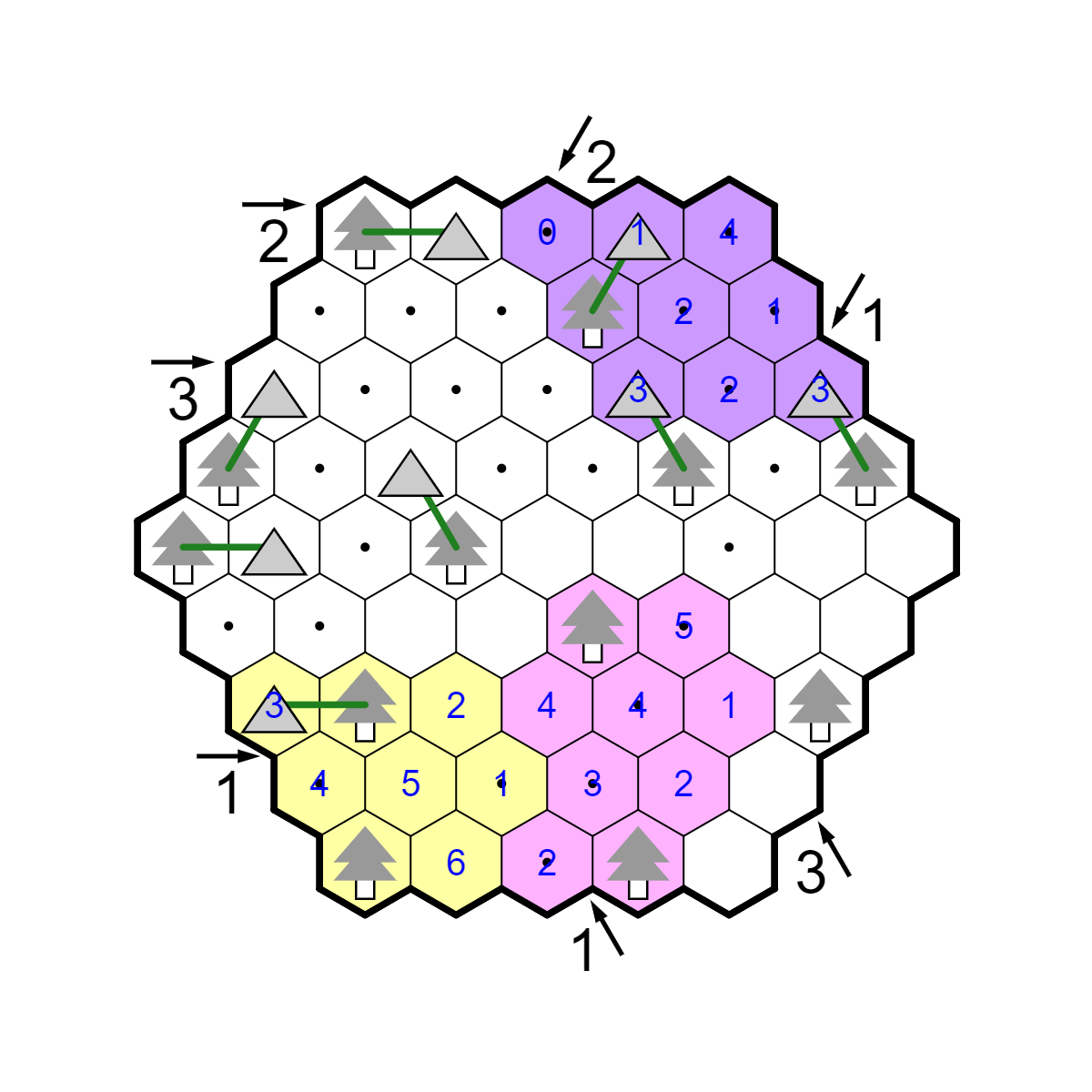
The next step involves the 3 up-left clue. There is already one
tent along that line, and there are only two more trees that are
close enough to have their tent there. So this means R6C5's tree connects
to a tent on R5C6, and there's a tent in one of R7C6 and R8C6. But
similar to the earlier deduction, the tree on R9C4 means there cannot
be a tent on R8C6, so this resolves both of these trees. Finally,
the 1-right clue resolves the final tent on R8C2.
Uso-One
In this solution, we use an O on top of a clue to mark that it must
be telling the truth, while an X marks that it must be lying.
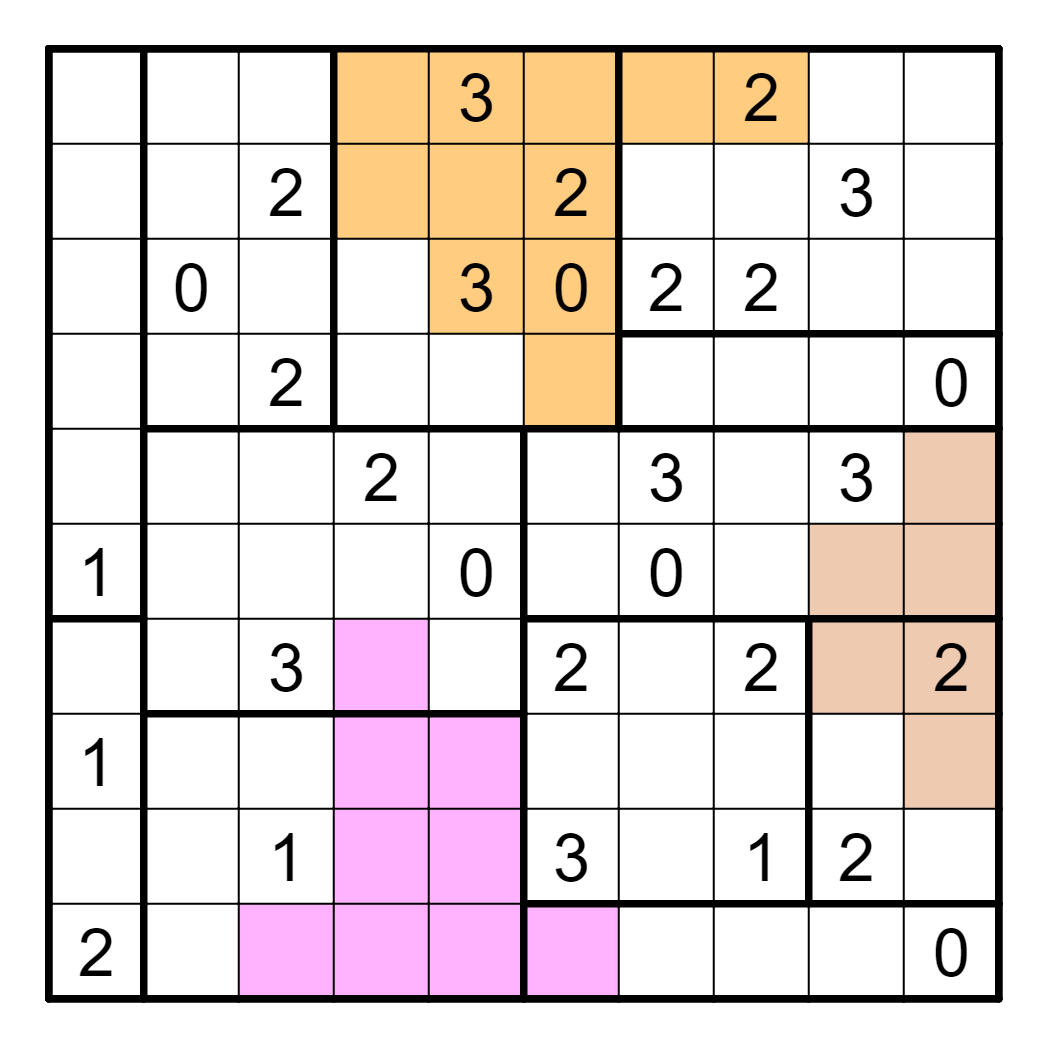
In Uso-One, some clues are known to be liars. For instance, a 3 on
the edge cannot be a truth teller because if it were true then
that cell would be separated from the rest; there is a similar issue
for 2s in the corner. This immediately resolves the liar in two regions.
Then, because R3C5 is a 3-clue and R3C6 cannot be shaded, we get three
shaded cells immediately. Also, note that some clues are the only one
in their region, which makes them liars by default.
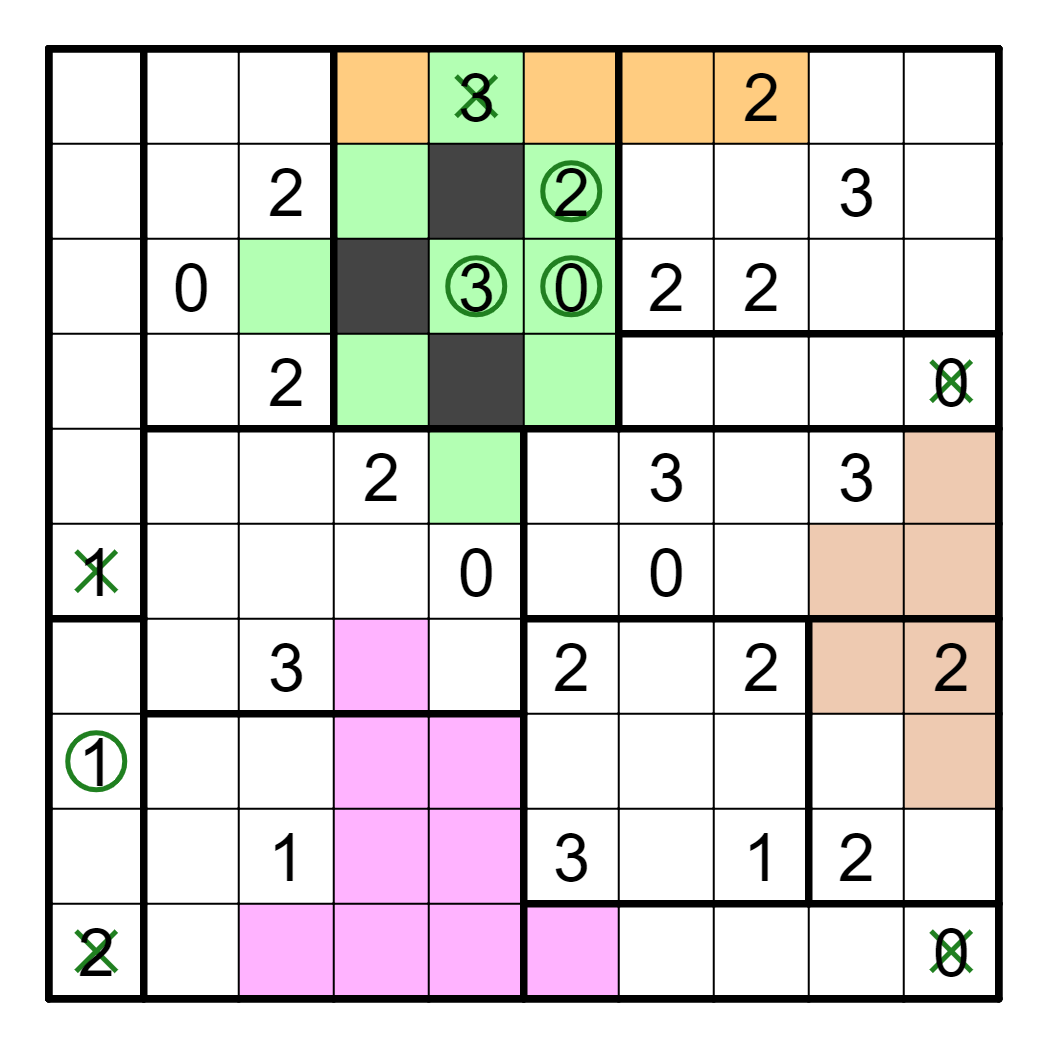
Consider the region containing the 2,0,2. If the top 2 is true, then the 0
is lying, and vice versa. Similarly, if the bottom 2 is true, then the 0
is lying, and vice versa. Thus, if the 0 were true then both 2s would be
lying, so this isn't the case and both 2s are true. We can also apply
connectivity of unshaded cells to get R3C1 to be unshaded.
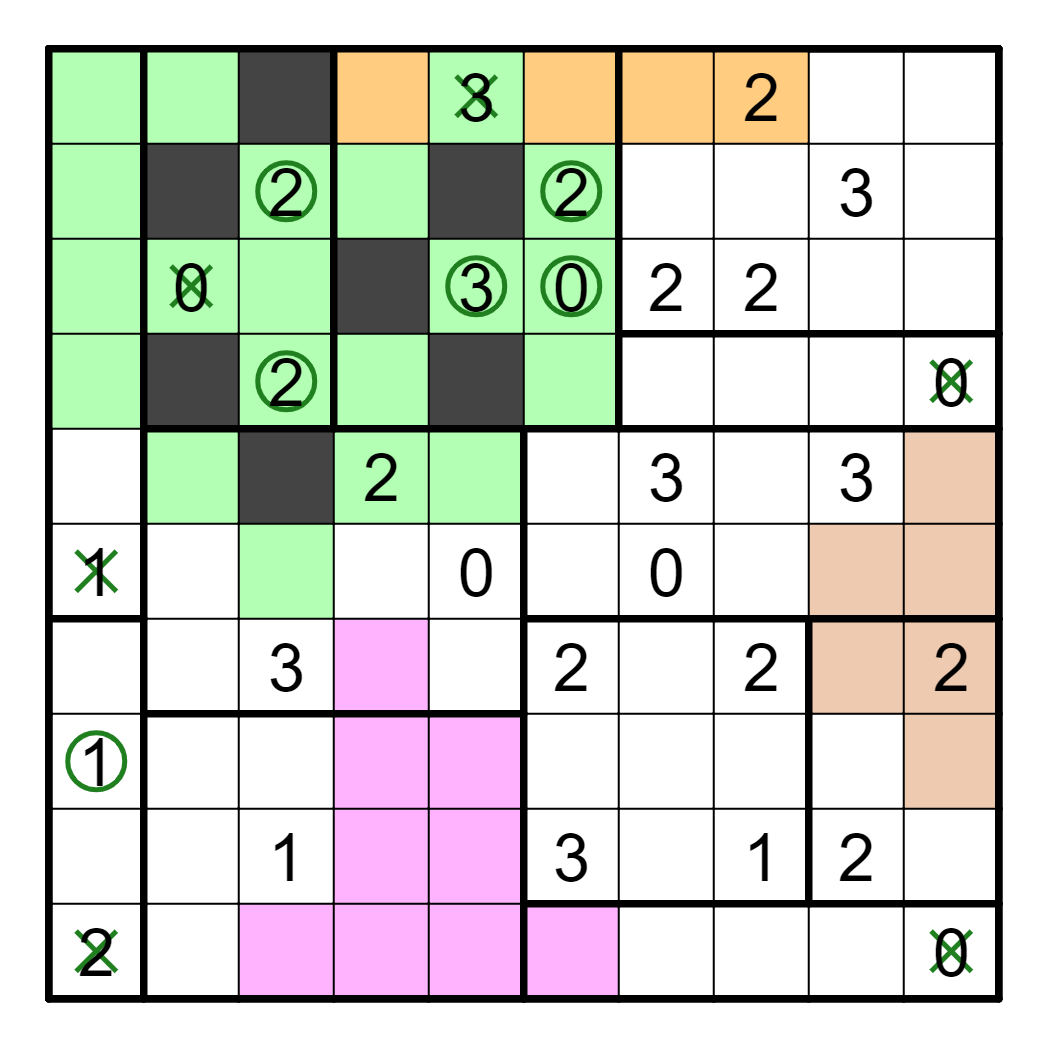
Now, consider the 2 and the 0 in the 2,0,3 region. Exactly one of these must
be true, since if the 2 is true then R6C4 is shaded and if the 0 is true
then it's unshaded. Thus, the 3-clue in R7C3 is always true. This shades
some cells which then resolves that the 0 is true and the 2 is lying.
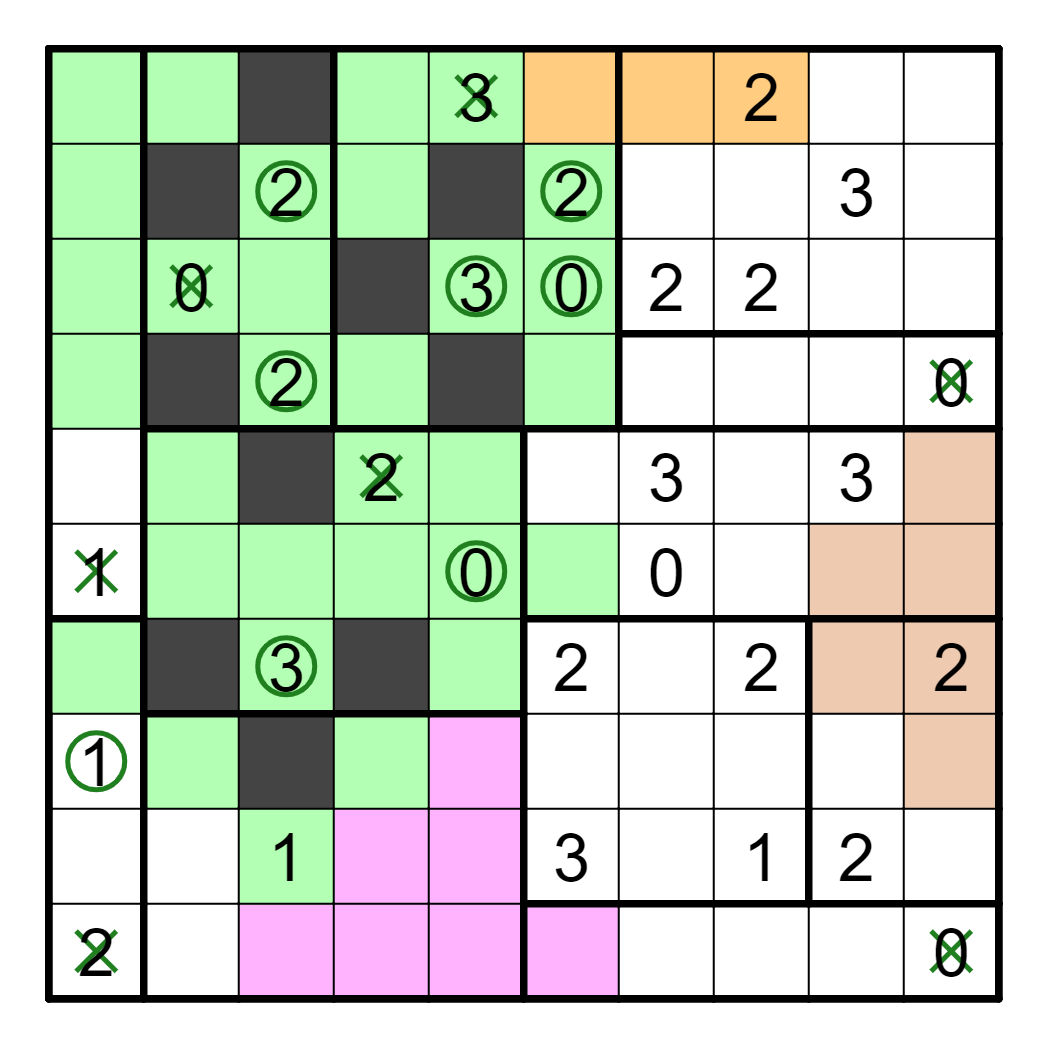
A similar deduction can be made on the top right region. The 2 in R3C7
is either lying or telling the truth. If it is true, then the 2 in R3C8
cannot be satisfied, so one of those two is a lie, which means the other
two clues in the region are definitely true. Then, to avoid breaking
connectivity, R1C9 and R2C10 cannot both be shaded, which means R2C8
and R3C9 are shaded. This implies that R3C7 is lying, and we can resolve
a bit more based on the fact that the 0-clue nearby is definitely lying,
as well as using the 2-clue from R2C6.
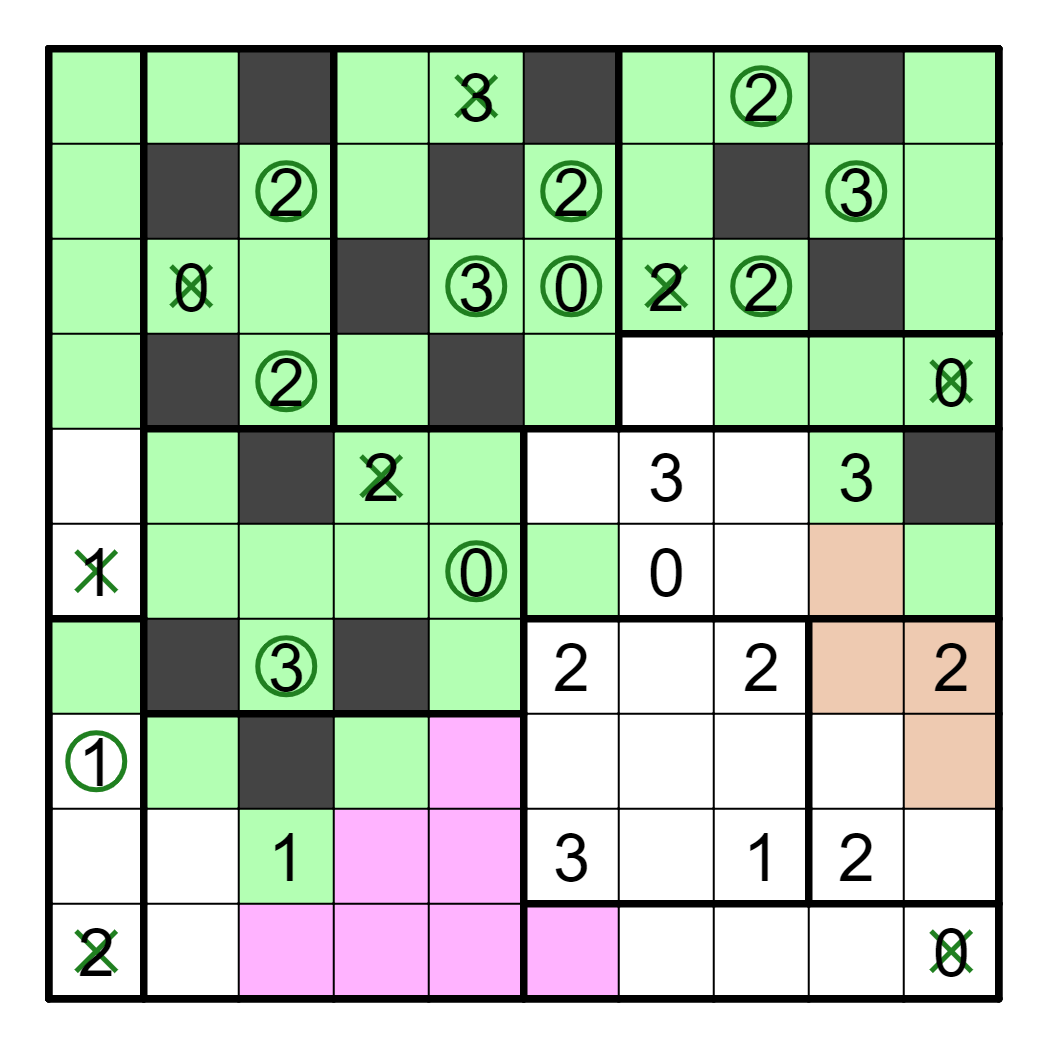
There is a rather subtle step now; consider the region with 3,3,0. If both
3s are true, then they are both resolved, but this breaks connectivity,
separating out the top right region from the rest. Thus, the 0 must be
true, and one of the 3s is lying. This, in turn, means that R7C6 must
be lying. Much of the bottom right gets resolved using the three
true clues there.
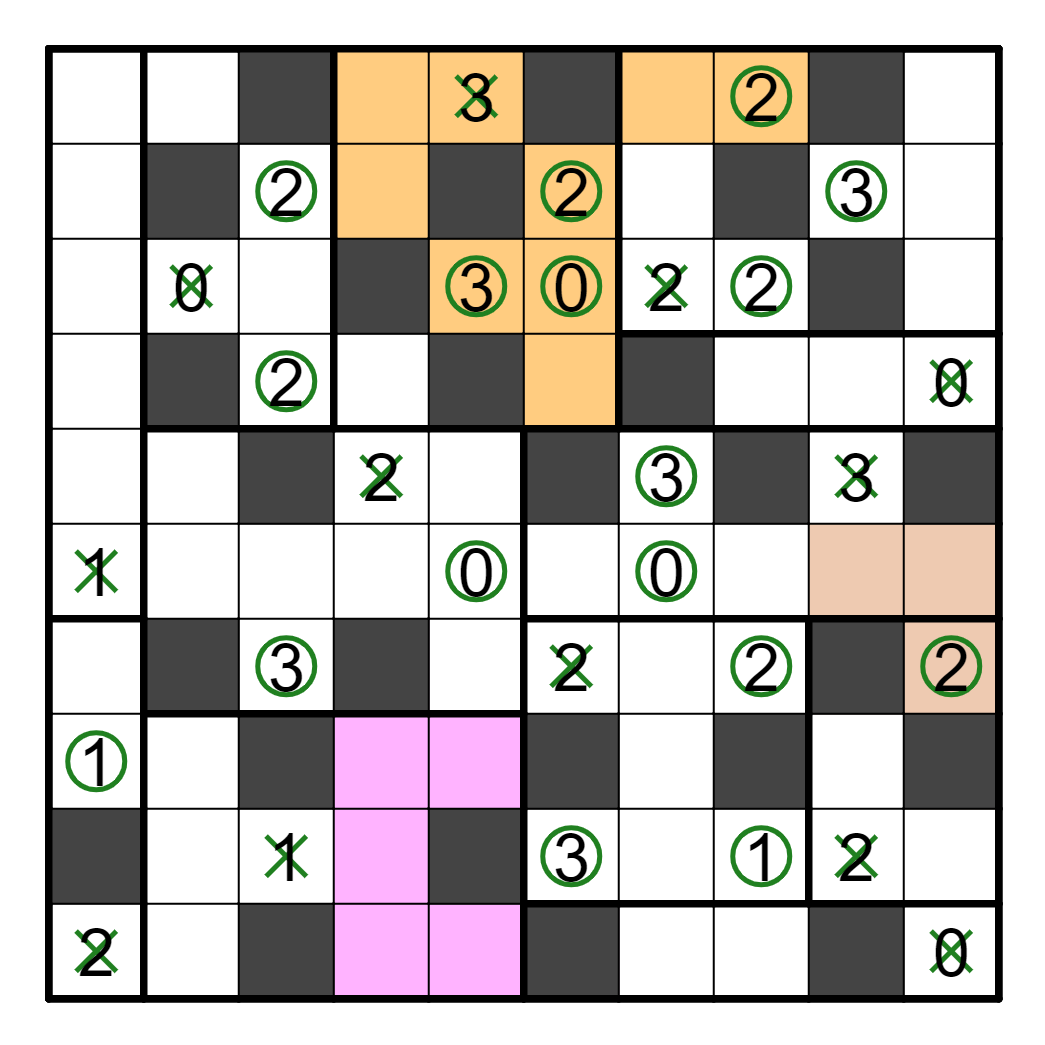
The 3s are resolved too, with R5C7 being true. Because the 2 in R9C9 being
true would break connectivity, it's false, which, along with the 0 being
wrong, resolves that section. Finally, the bottom left is also easily
resolvable, since R9C3 and R6C1 must not be satisfied.
Yajilin
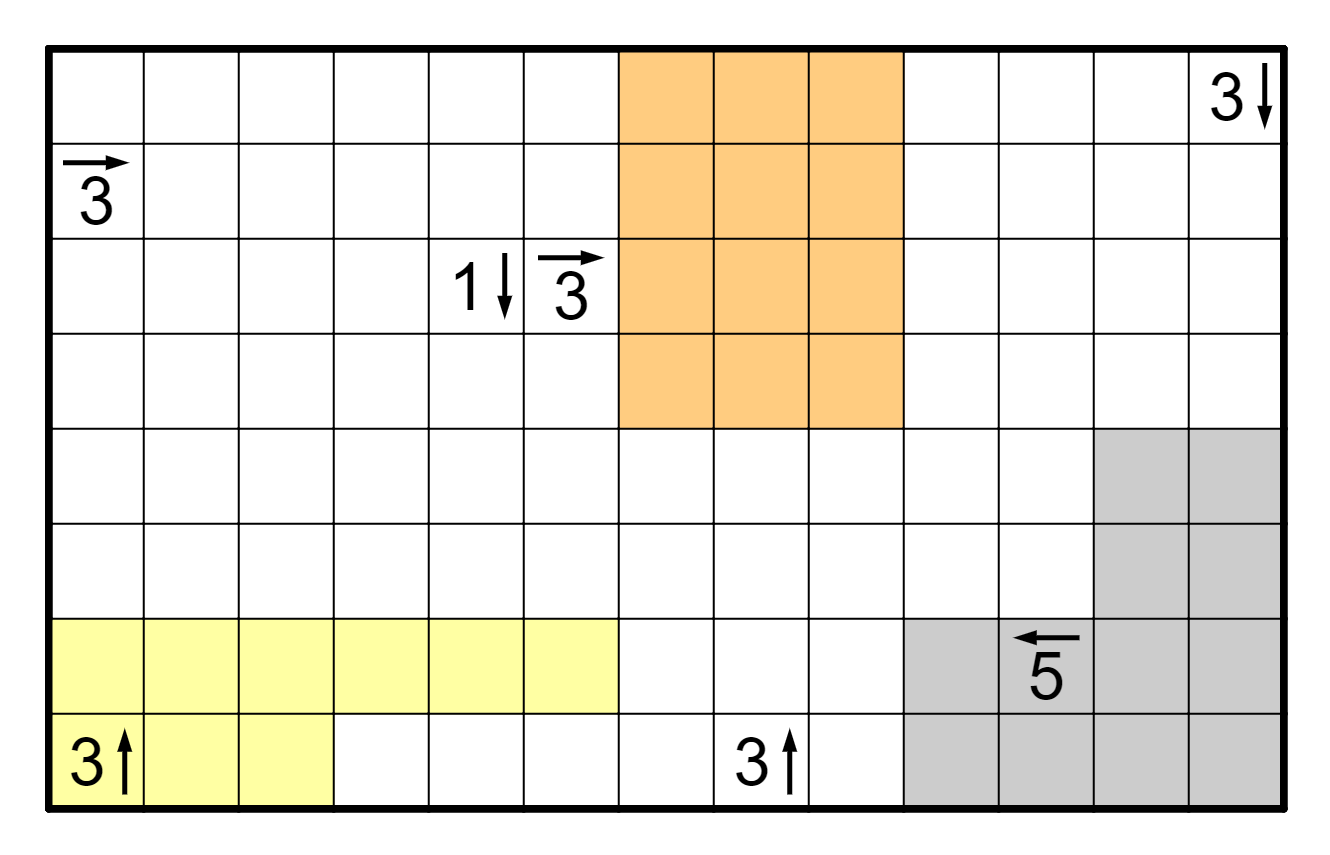
We can resolve quite a bit of this puzzle immediately by some Yajilin
counting deductions. First, the right column can be entirely
resolved. This is because on an edge, no two shaded cells can be
one cell apart from each other (or adjacent), so they have to be at
least two apart, which resolves it to be in Rows 2, 5, and 8. In addition,
Column 1 is similarly resolved; there must be a shaded cell in Row 1,
and then there cannot be one in Columns 4 or 6. In order to force three
in that column, they must be in Columns 3 and 7. We can draw a bit of the
loop based on these shaded cells.
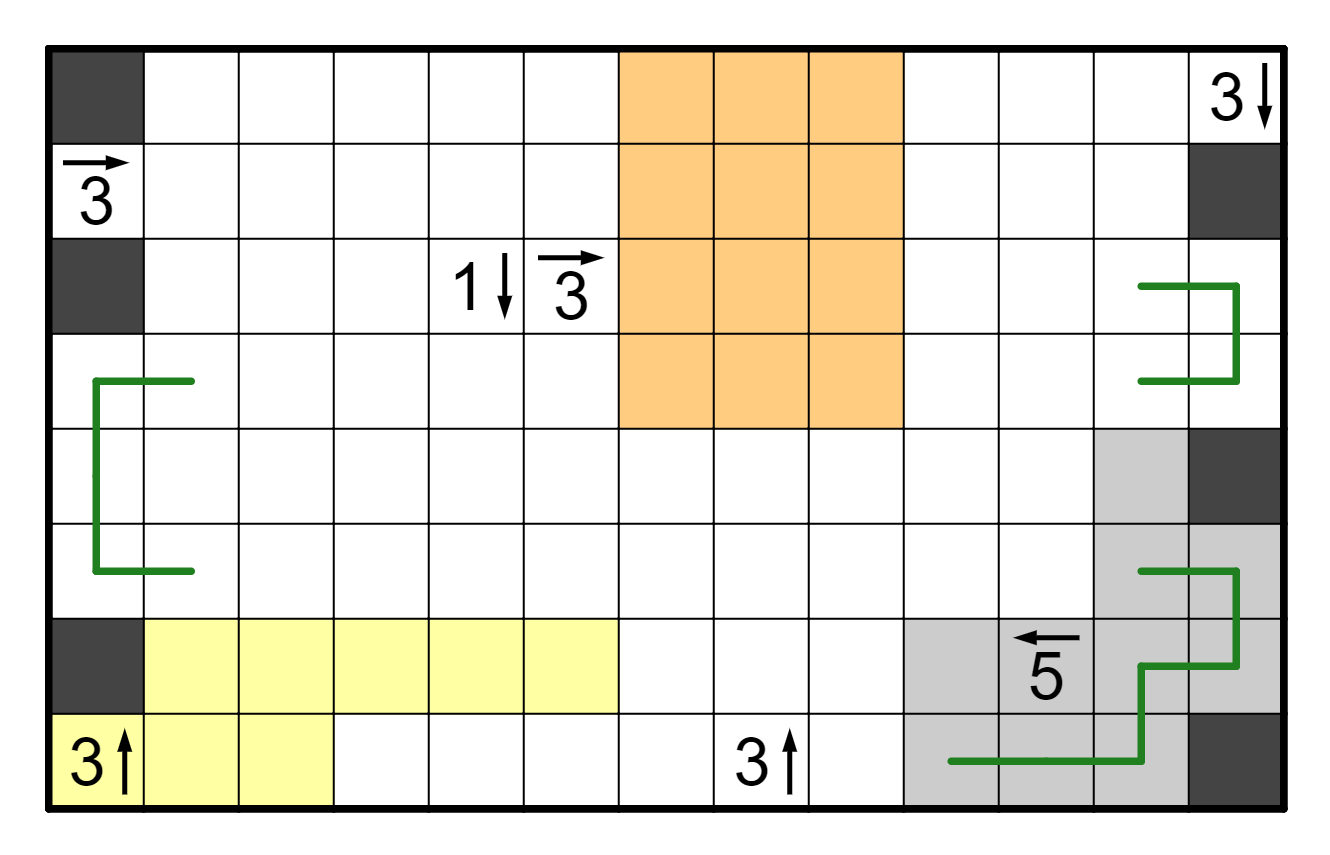
In fact, the 5-left clue can actually be fully resolved. Because we must
put five shaded cells within 10 cells, one in each pair is shaded, which
means R7C8 and R7C10 are shaded. Furthermore, consider what happens if,
say, both R7C3 and R7C5 are shaded. Then R8C4 is a problem, because
it has three directions it's forced to go out of. Similarly, if R7C4 and
R7C6 are both shaded, then R8C5 is broken. Thus, it must be the case that
both R7C3 and R7C6 are shaded.
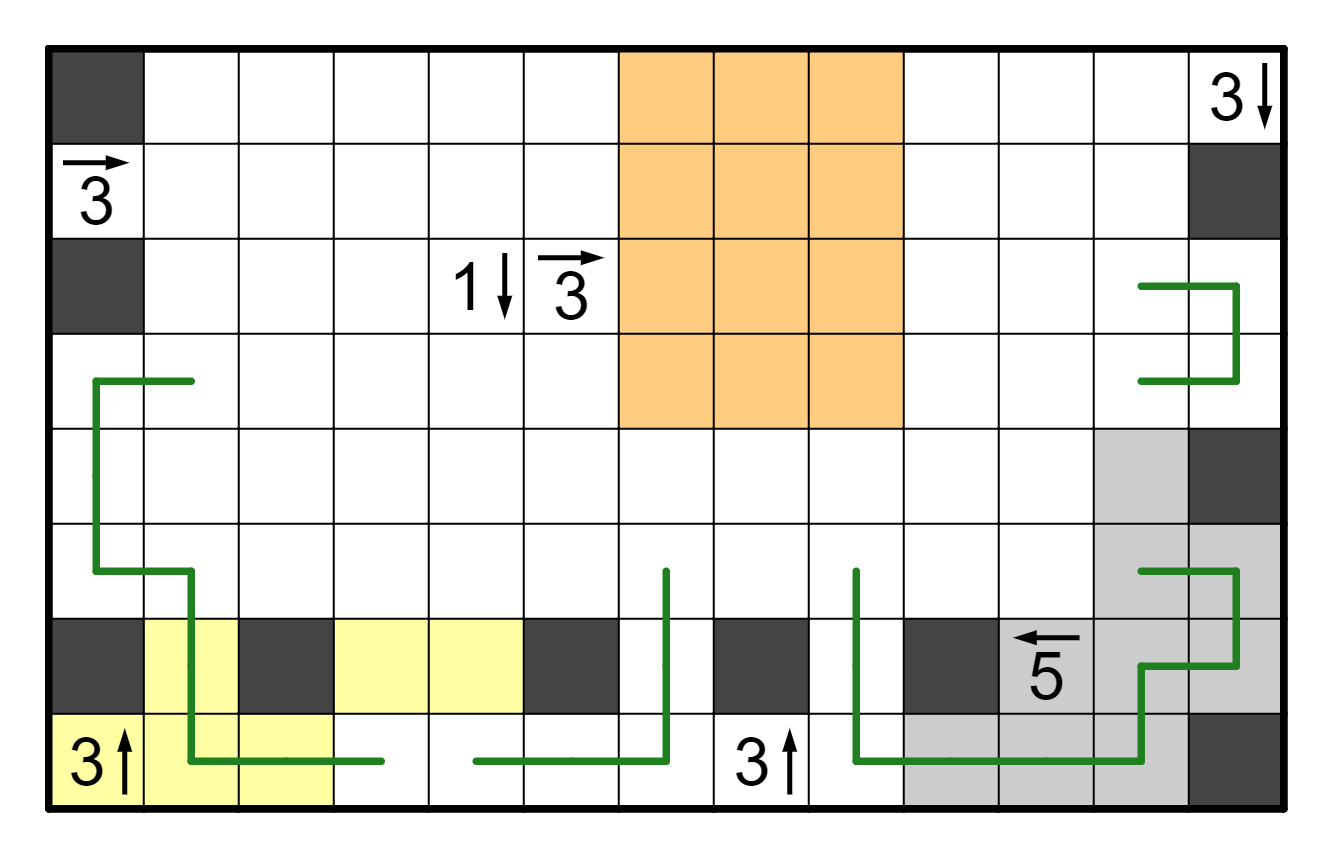
From here, the 3-right in R3C6 is also resolved, since there are only
five cells that can be shaded. After doing that (and resolving R3C8,
which has to go up and down), the 3-up is also immediately resolved,
which has more basic deductions we can make from there.
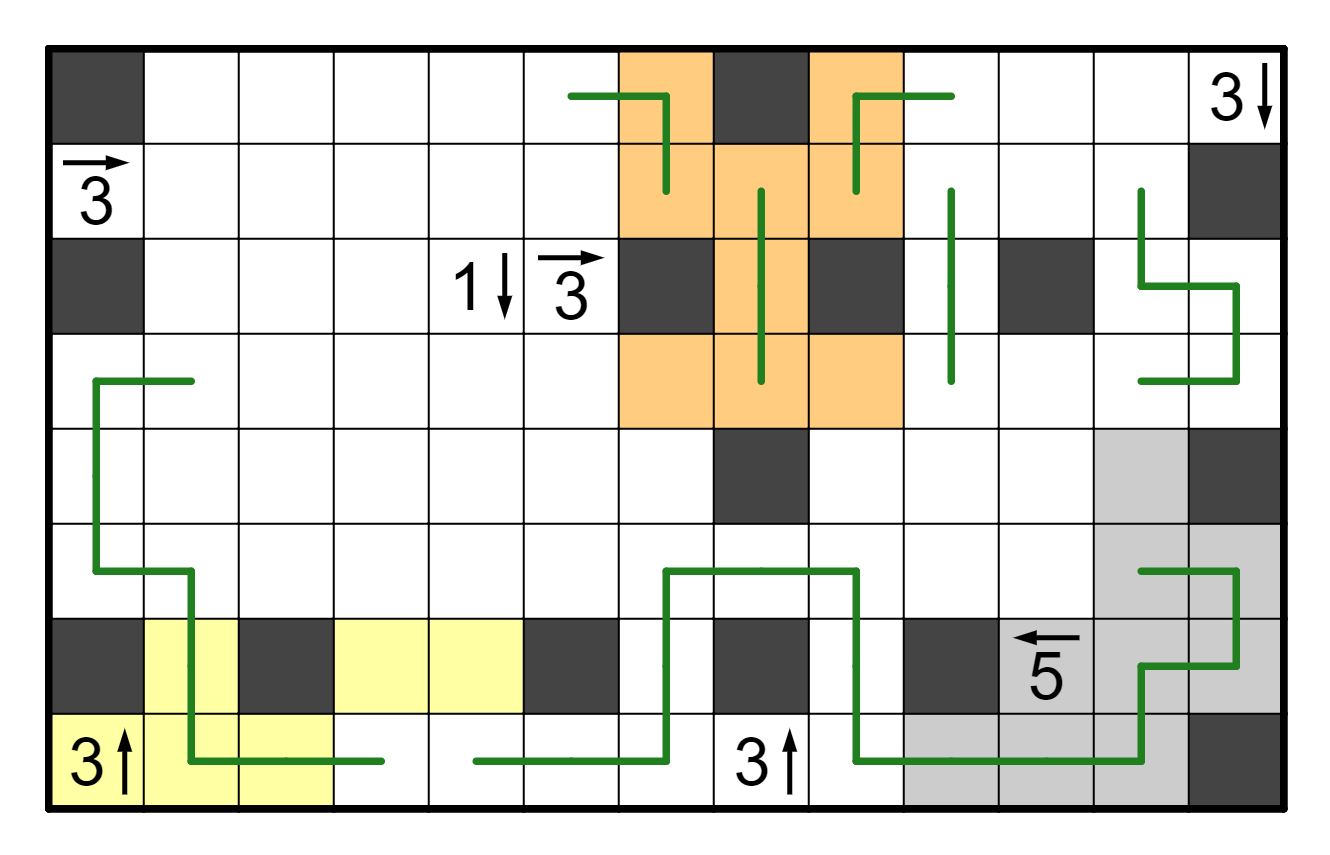
Now, we can do some entrance-counting deductions. Consider the bottom
right region. It currently has three entrances (R4C10, R4C12, R6C12),
and one possible-entrance (R4C8). If R4C8 goes left, then there is an
odd number of entrances in the bottom right, which means there will
definitely be one that is left unpaired. This is a problem, so R4C8 goes
right, and we can resolve a bit more because the cells adjacent to the
shaded ones are immediately resolved. By a similar token, R2C8 must
go left to satisfy parity, which resolves the top right, and to avoid
a smaller loop, the right side is resolved entirely.
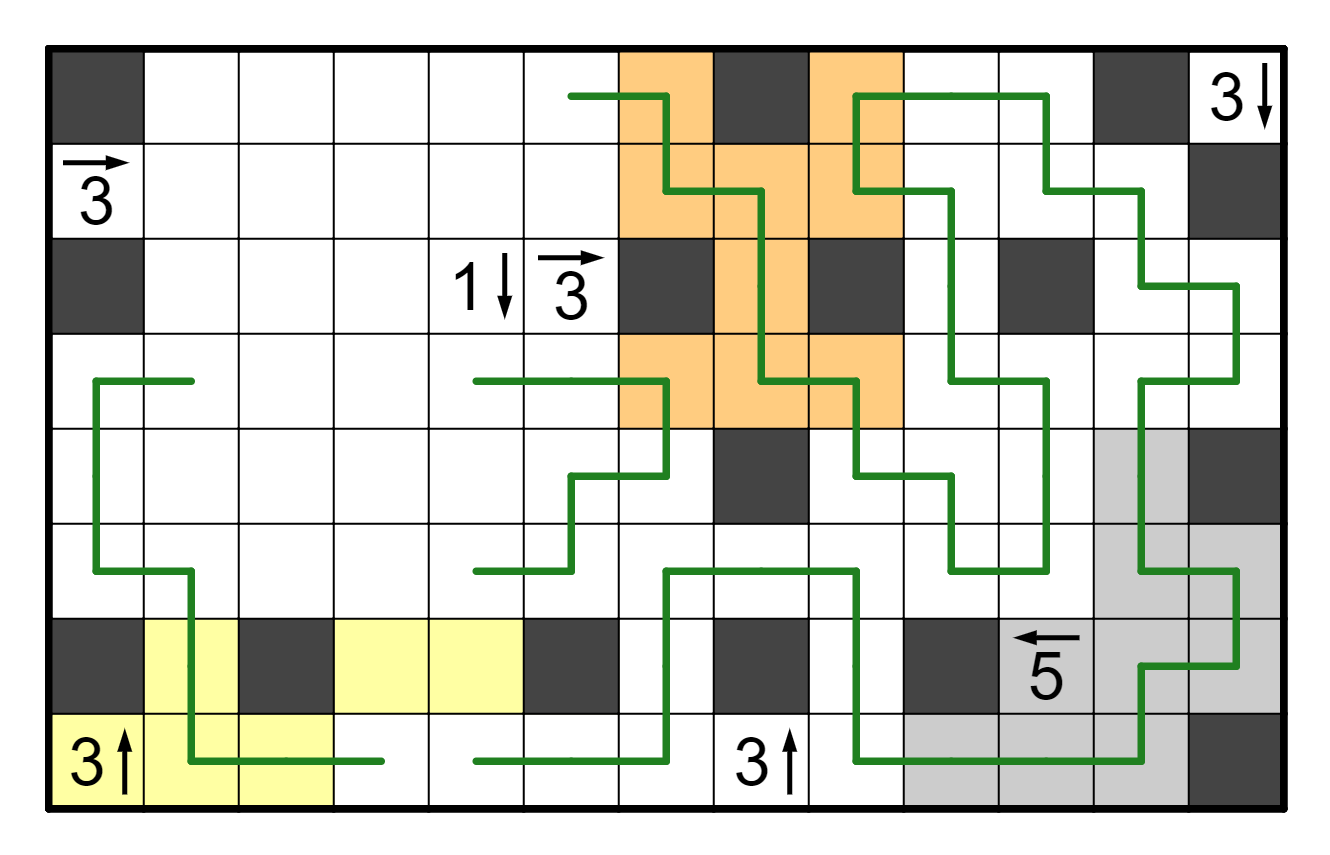
The 3-right in R2C1 is actually resolved; by the same deduction as
the 5-left, we can't have two cells that are one space apart that are
both shaded, and R2C2 can't be shaded because if it were then R1C2
is trapped, so R2C3 and R2C6 are shaded. Also, the 1-down is
resolved too, since R7C5 can't have a shaded cell, so R5C5 must have one.
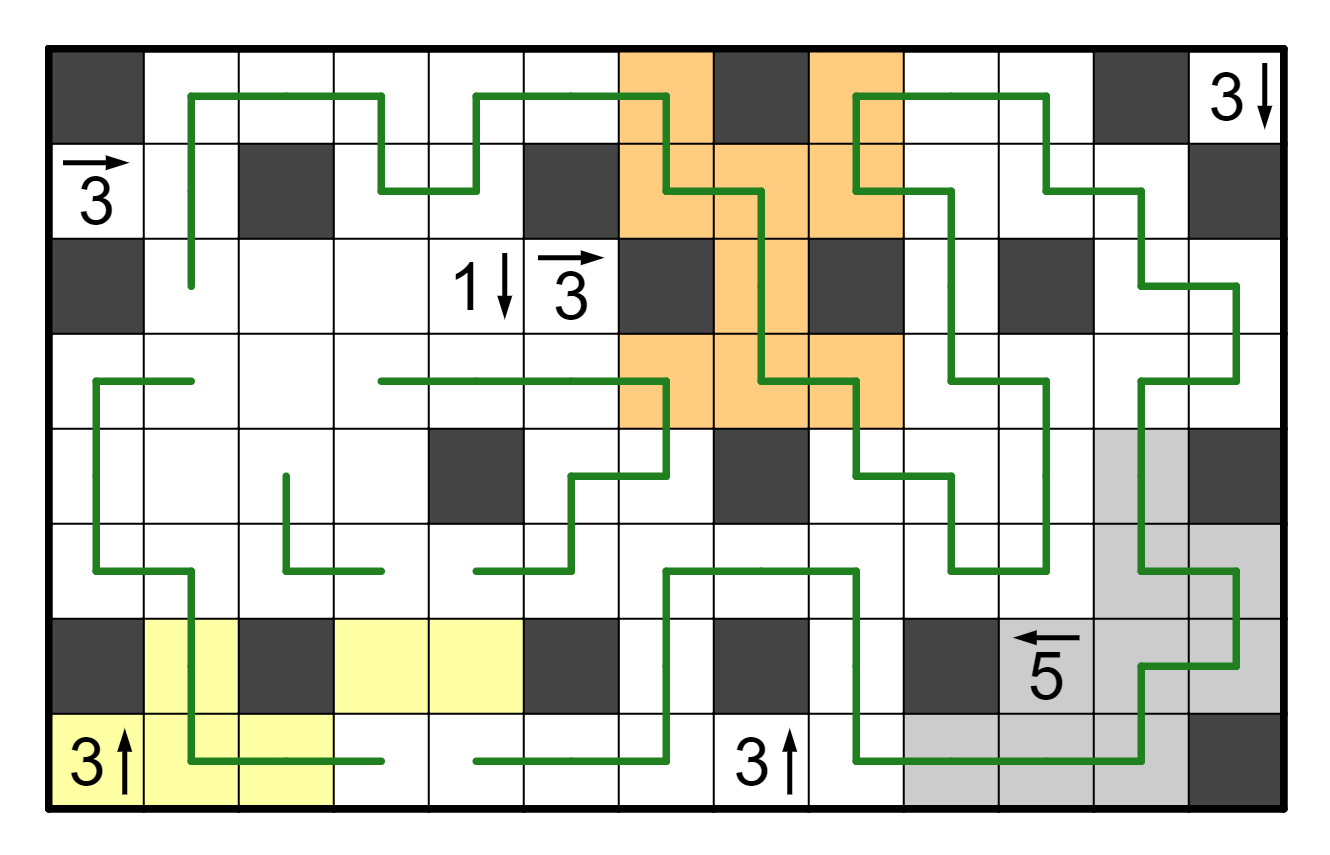
One final entrance-counting deduction solves the puzzle. Consider R6C4.
If it goes up, then there are an odd number of entrances to the bottom
unresolved section, which is bad. Thus it can't go up, but this means that
R5C4 must go both up and left. The rest of the puzzle resolves immediately
from there.
Sudoku
Unlike the others, this puzzle is computer-generated; it's also very
straightforward, and only requires simple deductions, either "This number
can only go in one place" or "Only one number can go here".
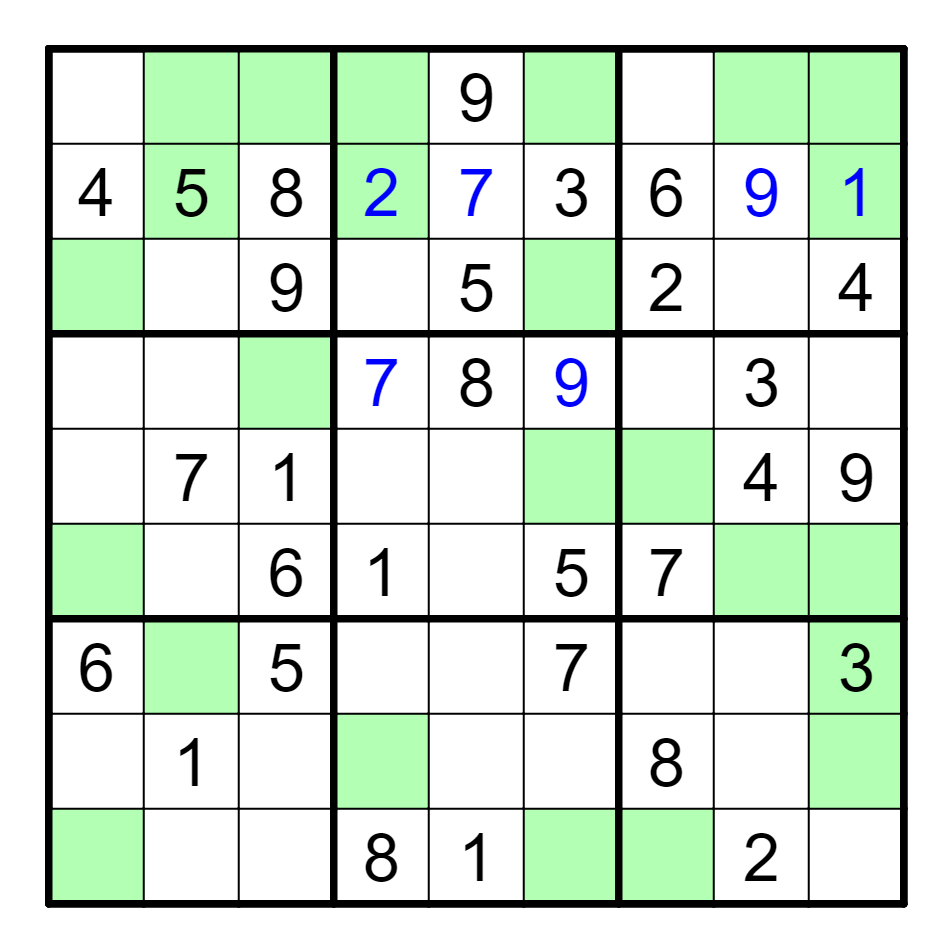
There are a lot of clues that can immediately be filled in. 7 in Box 5
must be in R4C4, and after this, 7 must be in R2C5 in Box 2. 9s are forced
in R4C6 and R2C8 in their respective boxes. The 7 and 9 in Row 2 let
us resolve that row; R2C4 has a 2 and R2C9 a 1.
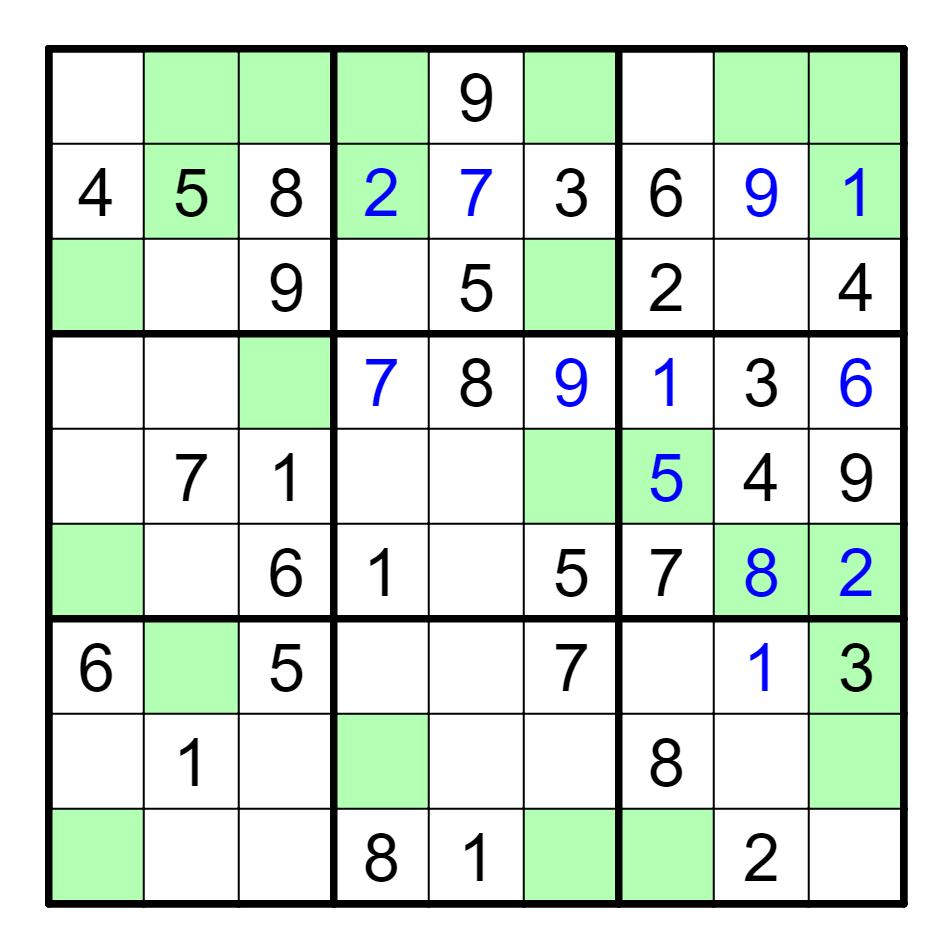
The 1 now places a 1 in R4C7 and R7C8. Also, 6 is forced into R4C9 in
box 6. The rest of the box resolves immediately, with the 2 and 5 only
having one spot each.
All of the 8s can now be resolved; Box 3 has only one spot, then Box 2,
and similarly Box 4 only has one spot and Box 5 only have one
spot each. Also, Box 3 gets resolved, with the 3 being placed,
and then the 5, with the 7 going in the final spot.
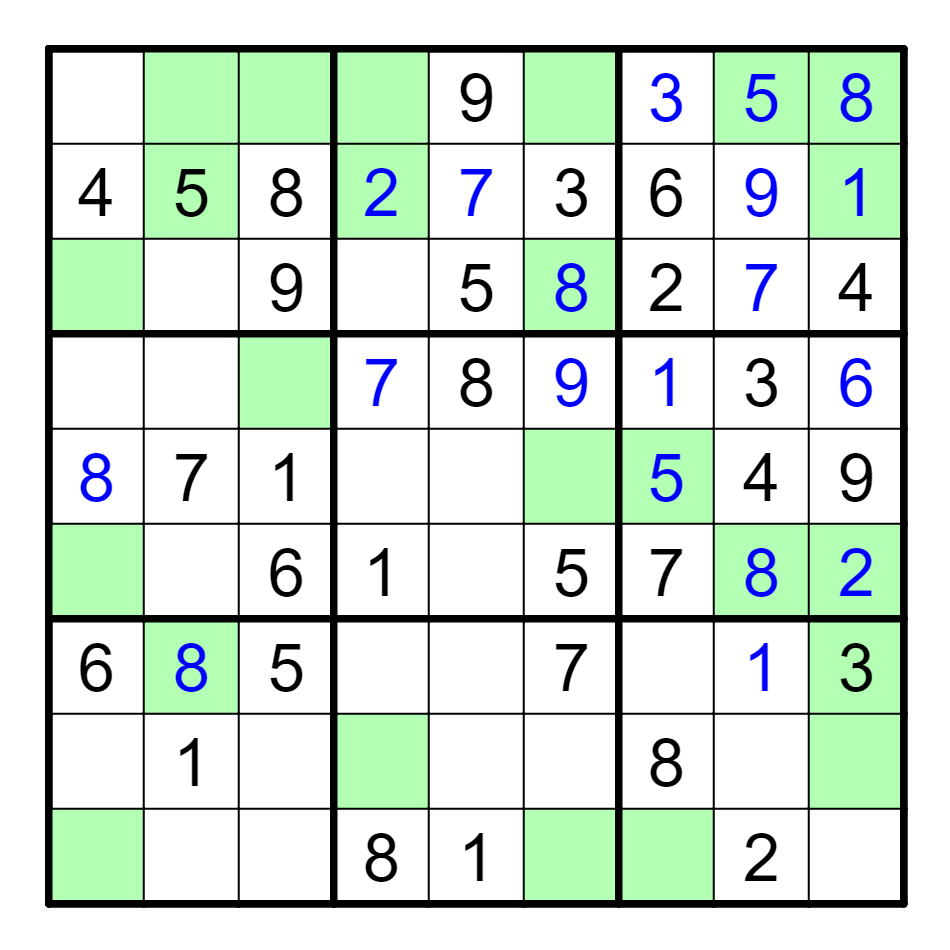
The remaining 1s can also get resolved because Box 2 only has
one spot for a 1. Box 2 also gets resolved by the 4 going to R4C1.
After placing a 6 in R3C4, the 6s can be entirely resolved in the grid.
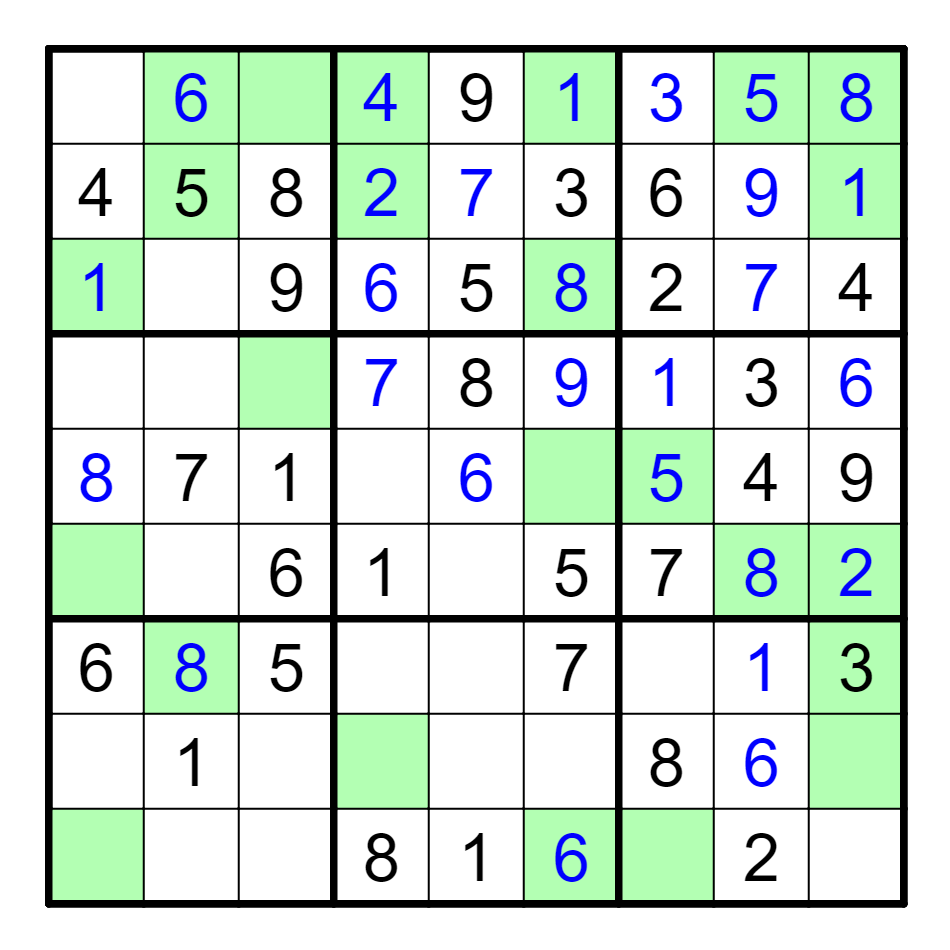
We can now place 3s in Box 1, 4, 5, 8, and then 7, resolving the 3s. Then,
we can resolve the remaining 5s in Boxes 4, 8, and 9. This now resolves a
7 in Box 9, which gives all of the 7s, and from there the rest of the
puzzle resolves the remaining digits straightforwardly.