The Pittsburgh Weather Puzzle
Answer: MATADOR
Looking over the whole dataset, it really is impossible to win;
there aren't any contiguous sequences of 7 sunny days anywhere in the past 4 years,
much less a sequence that matches all of the ideal temperatures exactly.
Thus, we deduce that the goal of the puzzle is to discover the temperatures in the ideal week
without actually winning the game, i.e. through the actions of the computer only.
Note the control that limits the computer's path length; we can discover each day's ideal temperature by starting the path length at 1, then setting the path length to 2 and using the first day to figure out the second, etc. all the way up to 7. There are many ways to "solve" each day; the below just supplies an example solution.

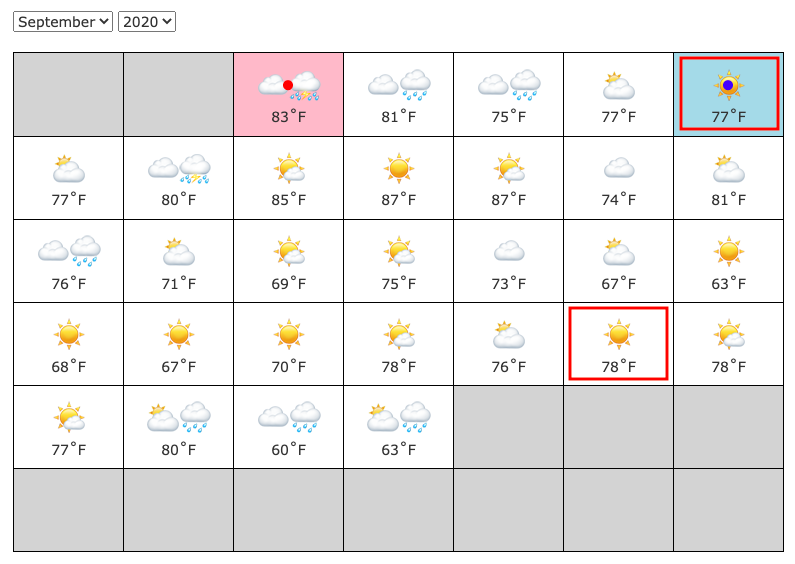
With this in mind, we can set up "queries" of whether the second day is ≥ or < a given point on the calendar. For example, this restricts the day 2 temperature to < 66:
While this restricts the day 2 temperature to ≥ 65:

Which settles the second day at 65 degrees.

By this point, you may be able to guess the answer already, but let's continue on in case it's still too ambiguous.

However, it's probably just easier at this point to keep using the weather interval lemma. As long as the two points in the middle have the same temperature or are both less/greater than the second and third day temperatures, they will not make a difference in the point values when read forwards versus backwards. This restricts the fourth day to ≥ 65, which gives us 65 as our final result.
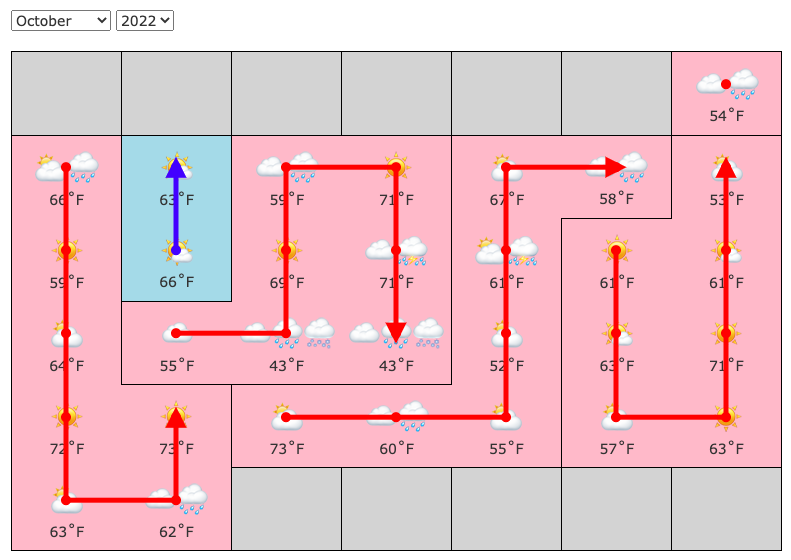
Another potential idea is to force a path of length 7 to make a choice right in the middle. For example, this restricts the fourth day to ≥ 62.
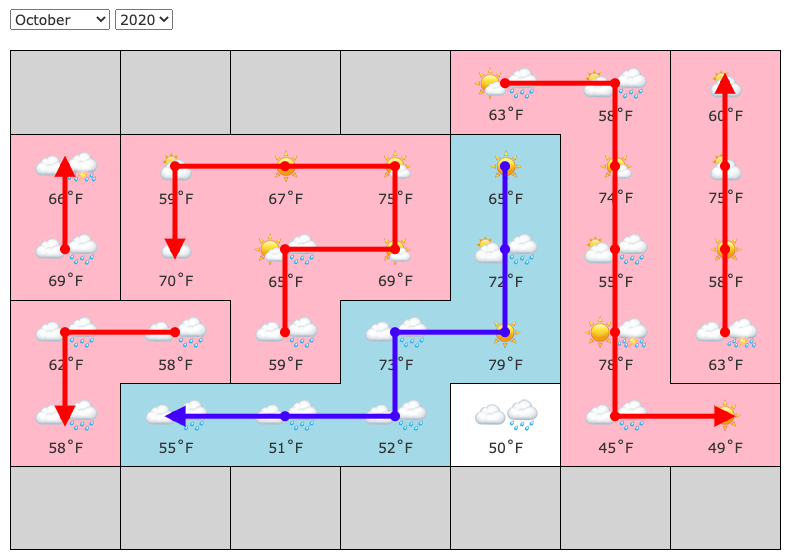
The benefit of this is that you don't need to worry about any other temperatures, whether in the calendar or in the ideal week. However, it takes a lot of room (relatively) to set up, and it's hard to find places to set this up to make a useful choice.
By this point, you have enough temperatures to guess the final answer with a decent level of certainty (the answer is the first result on Nutrimatic by now). However, just for the sake of finishing, let's keep going.
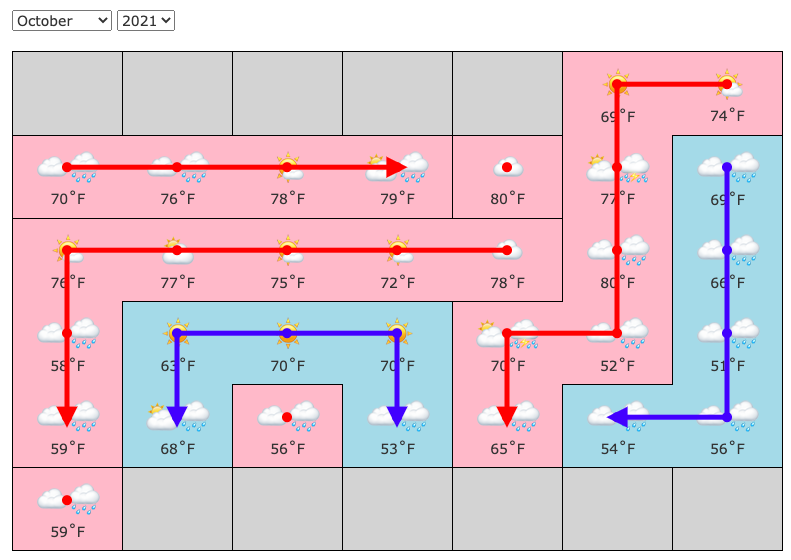
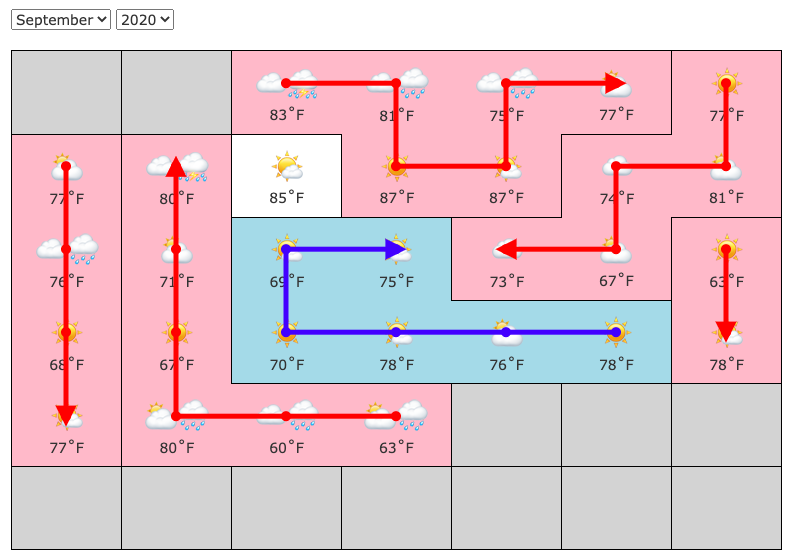
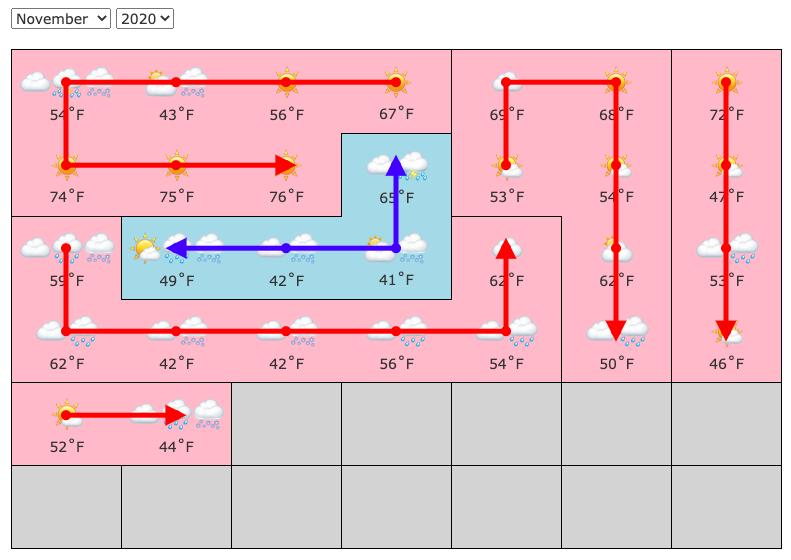
However, once you've narrowed it down to a handful of different temperatures, it becomes increasingly hard to find somewhere to set this up to make a useful choice, so bringing the weather lemma back into play might help at the end (e.g. this narrows day 6 to > 78, making the final result 79).

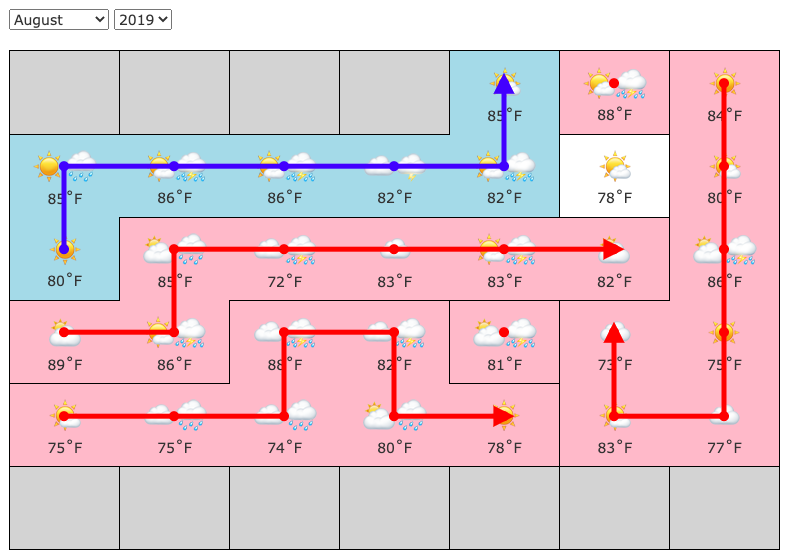

And we're done!
Note the control that limits the computer's path length; we can discover each day's ideal temperature by starting the path length at 1, then setting the path length to 2 and using the first day to figure out the second, etc. all the way up to 7. There are many ways to "solve" each day; the below just supplies an example solution.
Day 1:
Here, the easiest way is to just see which days the computer prefers. Since the computer prefers 77 (sunny) over 76 (sunny) and 78 (sunny), the first day must be 77 degrees.

Day 2:
Here, we have to be more intentional. Looking at the double-arrow control, we can prove the following lemma:
Weather interval lemma:
Suppose the computer draws a 2-length path on the calendar, where both endpoints are colder than the first day's known temperature and the second day's temperature is unknown. Since the points allocated for the weather conditions (e.g. sun/rain) do not change based on path index, they do not matter in determining whether the direction of the path makes a difference; only the temperatures matter. Specifically, the direction with less total absolute difference will win, or if the sum of the absolute temperature differences is the same, they will tie. We draw the three known temperatures on a number line, where the open circle is the first day's temperature and the closed circles are the temperatures of the endpoints.
Suppose the second day's temperature is also hotter than both endpoints.
Then, we can see that, no matter which endpoints the days are matched with,
the total temperature difference is the same, and the two directions will tie,
resulting a double arrow.
Suppose, then, that the second day's temperature is between the endpoints.
Now, the direction does make a difference, and the latter assignment below will
"win", resulting in a single arrow rather than double arrow.
Finally, suppose that the second day's temperature is lower than both endpoints.
Direction still makes a difference here, resulting in a single arrow.
In the end, we find that a double arrow corresponds to the second temperature
being at least as hot as the hotter endpoint, and a single arrow corresponds
to the second temperature being cooler than the hotter endpoint.
(We can similarly show a symmetric result where the first day's temperature
is cooler than both of the endpoints.)
This can be extended to any path on the calendar where the middle (i.e. non-endpoints) of the path has an equal point value read forwards or backwards.
Suppose the computer draws a 2-length path on the calendar, where both endpoints are colder than the first day's known temperature and the second day's temperature is unknown. Since the points allocated for the weather conditions (e.g. sun/rain) do not change based on path index, they do not matter in determining whether the direction of the path makes a difference; only the temperatures matter. Specifically, the direction with less total absolute difference will win, or if the sum of the absolute temperature differences is the same, they will tie. We draw the three known temperatures on a number line, where the open circle is the first day's temperature and the closed circles are the temperatures of the endpoints.
This can be extended to any path on the calendar where the middle (i.e. non-endpoints) of the path has an equal point value read forwards or backwards.
With this in mind, we can set up "queries" of whether the second day is ≥ or < a given point on the calendar. For example, this restricts the day 2 temperature to < 66:

While this restricts the day 2 temperature to ≥ 65:

Which settles the second day at 65 degrees.
Day 3:
Since the middle element has the same point value read forward or backwards, we can use the weather interval lemma again without worrying about the second day at all. For example, this settles the day 3 temperature at 84 degrees:
By this point, you may be able to guess the answer already, but let's continue on in case it's still too ambiguous.
Day 4:
Now that the path is a bit longer, it's easier than before to make judgements based on the computer's path itself, rather than relying on the double arrows. For example, this restricts the fourth day to ≤ 65:
However, it's probably just easier at this point to keep using the weather interval lemma. As long as the two points in the middle have the same temperature or are both less/greater than the second and third day temperatures, they will not make a difference in the point values when read forwards versus backwards. This restricts the fourth day to ≥ 65, which gives us 65 as our final result.

Another potential idea is to force a path of length 7 to make a choice right in the middle. For example, this restricts the fourth day to ≥ 62.

The benefit of this is that you don't need to worry about any other temperatures, whether in the calendar or in the ideal week. However, it takes a lot of room (relatively) to set up, and it's hard to find places to set this up to make a useful choice.
By this point, you have enough temperatures to guess the final answer with a decent level of certainty (the answer is the first result on Nutrimatic by now). However, just for the sake of finishing, let's keep going.
Day 5:
Again, we could set up the calendar such that the computer has to make a choice between two endpoints. However, notice that the temperatures in the new "middle" of the path are 65-84-65. That is, the direction of the path again does not make a difference in the point value of the path's middle, and we can use any 5-length path with the weather interval lemma without worrying about satisfying any conditions. This makes it easy to set up a "query" of whether the temperature is higher or lower than something: all you have to do is make a path of length 5 to any lower temperature. For example, this restricts the 5th day temperature to ≥ 68 and < 69 on the left and right, respectively, making the 5th day temperature 68.
Day 6:
Now, the days in the middle of the path are so uneven that the only reasonable way to use the weather lemma is to find a bunch of days that are all higher than 84 or lower than 65. While narrowing down the temperature, it might just be easier to set up these kinds of things (e.g. this narrows day 6 to ≤ 80):
However, once you've narrowed it down to a handful of different temperatures, it becomes increasingly hard to find somewhere to set this up to make a useful choice, so bringing the weather lemma back into play might help at the end (e.g. this narrows day 6 to > 78, making the final result 79).

Day 7:
Finally. These narrow the final day to 82.

And we're done!